A Look at the Power Rating of Resistors

You may be asked: “what is the power rating of the resistors you want to buy?” when buying a resistor to build a certain circuit. For the most standard class of resistors, you may simply be given ¼ Watt resistor.

The power rating of a resistor is the specification given with a resistor that serves to tell the maximum amount of power that the resistor can withstand.

Thus, if a resistor has a power rating of ¼ Watts, ¼ Watts is the maximum amount of power that should be fed into the resistor.

When an electrical current passes through a resistor, electrical energy is lost by the resistor in the form of heat and the greater this current flow, the hotter the resistor will get. Heat is generated as the current passes through electrical components. The heat is usually negligible and unnoticed in a circuit if the current is small enough and suitable for the circuit. A substantial amount of heat in a circuit can be created if the current is large enough.

The reason why resistors are given power ratings is because current can melt components and possibly create shorts in a circuit if the maximum allowable amount of power that can pass through the resistor is not specified.

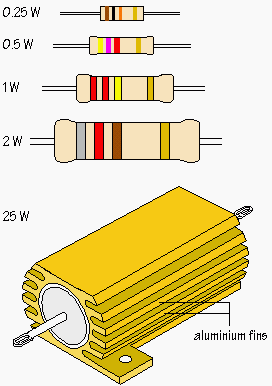
The Resistor Power rating is sometimes called the Resistors Wattage Rating and is defined as the amount of heat that a resistive element can dissipate for an indefinite period of time without degrading its performance. Depending upon the size, construction, and ambient operating temperature, the power rating of resistors varies a lot from less than one tenth of a watt to many hundreds of watts. For an ambient temperature of +70 degrees Celsius, most resistors have their maximum resistive power rating given.

Since the standard power ratings of 0.25W or 0.5W are suitable for most circuits, the power ratings of resistors are rarely quoted in parts lists. It should be clearly specified in the parts list for the rare cases where a higher power is required.

The Resistor Power Triangle

From Ohm’s Law, a product of power is produced when a voltage is dropped across a resistor and a current passed through the resistor. A Power Triangle superimposes the 3 quantities of power, voltage and current into a triangle since power is always consumed if a resistor is subjected to a voltage or if it conducts a current. The image below shows the power dissipated as heat in a resistor at the top and the current and the voltage at the bottom.

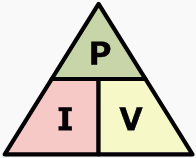
The above expression for the resistor power can produce two possible alternative variations if two of the values are known. The 3 standard formulas can be used to calculate the power dissipation of any resistor.

Where,

V – is the voltage across the resistor in volts
I – is the current flowing through the resistor in amperes
R – is the resistance of the resistor in Ohms