Ungrounded Grounding System
- Ungrounded system
- Derivation of current expression in ungrounded system
- Advantages & disadvantages of ungrounded system
- Concept of effective and non-effective grounding
- Coefficient of earthing and earth fault factor
Underground Neutral Or Undergrounded System
Before 1950 power system were often without neutral grounding. Such system had repeated arcing grounds, insulation failure and difficult earth fault protection.
Every phase has inherent distributed capacitance with respect to earth. If earth fault occurs on phase B, the distributed capacitance discharges through the fault. The capacitance again gets charged and gets discharged. Because of this sever voltage oscillation is reached in healthy phases.
These voltage oscillation causes stress on insulation of connected equipment.
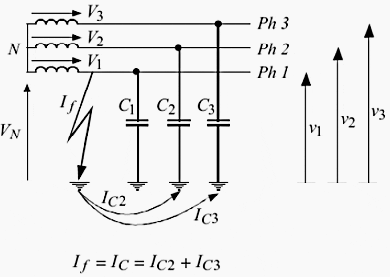
Ic2 = jCwv2
Ic3 = jCwv3
Ic = jCwv2 + jCwv3
Ic = jCw(v2 + v3) // Equation-01
Now by drawing the phaser diagram as shown below wecan write:
VN + V2 = v2 // Equation-02
VN + V3 = v3 // Equation-03
Substituting equation -02 and equation-03 in equation-01:
Ic = jCw(VN + V2 + VN + V3)
Ic = jCw(2VN + V2 + V3) // Equation-04
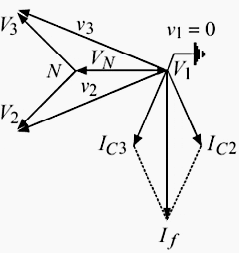
Voltage phasers V3 can be resolved in the direction of VN and in direction perpendicular to VN as V3Cosθ and V3Sinθ.
Similarly voltage phaser V2 can be resolved as V2Cosθand – V2Sinθ
Hence:
V2 + V3 = V3Cosθ + V3Sinθ + V2Cosθ – V2Sinθ // Equation-05
V3 = V2
V3Cosθ + V2Cosθ = VN
Substituting in equation-05 we get:
V2 + V3 = VN = V1 (Since V1 is shorted to ground soVN = V1) // Equation-06
Substituting equation-06 in equation- 04 we get:
Ic = jCw(2VN + VN)
Ic = j3CwV1
For ungrounded system:
If = IC2 + IC3 = IC = j3CwV1 // Equation-07
Since there is no return path available for fault current in ungrounded system so detection of earth fault current is difficult. This is other disadvantage of ungrounded system.
Advantages of Ungrounded System
There are some advantages of ungrounded system:
- Ungrounded system has negligible earth fault current
- Some continuous process or system and essential auxiliaries where single phase to ground fault should not trip the system.
Disadvantages of Ungrounded System
However below listed disadvantages of ungrounded system are more adverse than advantages:
- Unearthed system experience repeated arcing grounds.
- Insulation failure occurs during single phase to ground faults.
- Earth fault protection for unearthed system is difficult.
- Voltage due to lightning surges do not find path to earth.
In order to overcome the above mentioned technical and operation issues the concept of system grounding was introduced. System grounding is connecting the neutral of system to earth.
System grounding is of two types:
- Effective grounding: Effective grounding is also called solid grounding that is without resistance or reactance. In this case co-efficient of earthing ismore than 80%
- Non effective grounding: When neutral to earth connection is made through resistance or reactance than the system is said to be non-effectively grounded. In this case coefficient of earthing is greater than 80%
Coefficient of earthing and earth fault factor
Ce = Highest phase to ground voltage of healthy phase / Phase to phase voltage
In a system without neutral earth (refer Figure 1), phase to earth voltage phase-1 and phase-2 rises to 3times phase to phase voltage Vrms during single phase to earth fault on phase 3. In a neutral earthed system the voltage ofhealthy phase rises to Ce times Vrms.
Therefore value of Ce:
- For non-effectively earthed system Ce = 1
- For effectively earthed system Ce < 0.8. Hence surge arrester rated voltage is > 0.8 V rms
Surge voltage kV instantaneous is taken as 2.5 times of critical flashover voltage (CFOV) of line insulation. Thus discharge current is given as:
I = (2.5(CFOV) –Residual voltage of arrester) / Surge impedance of line
- V1 = Highest RMS phase to phase voltage of healthy phases (phase 2 and 3 refer to Figure 1) during earth faulton pahse-1
- V2 = RMS value of phase to earth voltage at same location with fault on faulty phases removed
References:
- Industrial electrical network design guide By Schneider electric
- Switchgear protection & power system By Sunil S Rao, Khanna publications
- EARTHING: Your questions answered By Geoff Cronshaw
- IEEE Recommended Practice for Electric Power Distribution for Industrial Plants
Copyright Notice
This technical article is protected by U.S. and international copyright laws. Reproduction and distribution of PDF version of this technical article to websites such as Linkedin, Scribd, Facebook and others without written permission of the sponsor is illegal and strictly prohibited.© EEP-Electrical Engineering Portal.
Related electrical guides & articles
Asif Eqbal
Bachelor of Engineering in Electrical & Electronics engineering, from Manipal University, (Karnataka), India in 2006. Presently involved in the design of EHV outdoor substation and coal fired thermal power plants for more than seven years. Motto of joining EEP as a contributor is to share my little engineering experience and help the budding engineers in bridging the conspicuous gap between academics and Industrial practice. “If you have knowledge, let others light their candles with it, so that people who are genuinely interested in helping one another develop new capacities for action; it is about creating timeless learning processes".Profile: Asif Eqbal
You need to correct the definition of VI in EFF , It should be
V1 = Highest RMS phase to Ground voltage of healthy phases (phase 2 and 3 refer to Figure 1) during earth fault on pahse-1
Yes, about ungrounded system this is very useful and your statement is proved actually on synchronous generator. V1=VN =V2> or V3>
information about ungrounded system was nice.apart from that information about system grounding was not clear.give complete information about that topic with diagrams so we are easily understand the concept.thank u.
Dear Asif!
I met ungrounded systems when i was commissioning engineer. There was 11/0,4 kV transformer with ungrounded 0,4 kV side. The cable to the ciruit breaker not too long, so capacitive earthing current not too high. What is the guaranty , the secunder voltage is below 1 kV to the earth? It could be possible 4-5 kV to the earth. Such kind of systems are working. Something is there what i don’t know.
Asif, I am practicing Electrical system auditor. Your articlke is very good and informative. Pl. follow by articles giving comparative advantages of diffrent grounding systems. Keep it up !
Thanks
Thanks for the explanation. I would like to know if there is effective protection method for unearthed system with high capacitance or a filter for EMI at the system??
Thanks, please give more explanation on effective and non effective grounding system. co-efficient of earthing is more than 80% in effective grounding and greater than 80% in non effective grounding system.
Great overview Asif! Looking forward to second ‘Grounded’ part!
Thank you, as you said i am budding engineer, please provide any books or materials on grounding
Use search box on top bar.
Congratulations, as always the content, photos and presentation of this website are outstanding. In this case when I saw the picture I asked “What would be the result of a electrical resistance testing by the four-point method to that connection?” Who knows … Greetings.