What is the complex power and how it figures in power analysis

Power absorbed by a given load

Considerable effort has been expended over the years to express power relations as simply as possible. Power engineers have coined the term complex power, which they use to find the total effect of parallel loads.

Complex power is important in power analysis because it contains all the information pertaining to the power absorbed by a given load.

Consider the AC load in Figure 1 above. Given the phasor form V = V_m∠θ_v and I = I_m∠θ_i of voltage v(t) and current i(t), the complex power S absorbed by the AC load is the product of the voltage and the complex conjugate of the current, or:

(1.10)

assuming the passive sign convention (see Figure 1). In terms of the rms values:

(1.11)

where

(1.12)

and

(1.13)

Thus we may write Eq. (1.11) as:

(1.14)

The complex power may be expressed in terms of the load impedance Z. The load impedance Z may be written as:

(1.15)

Thus, V_rms = Z × I_rms. Substituting this into Eq. (1.11) gives

(1.16)

Since Z = R + jX, Eq. (1.16) becomes

(1.17)

where P and Q are the real and imaginary parts of the complex power; that is,

(1.18, 1.19)

P is the average or real power and it depends on the load’s resistance R. Q depends on the load’s reactance X and is called the reactive (or quadrature) power.

Comparing Eq. (1.14) with Eq. (1.17), we notice that:

(1.20)

The real power P is the average power in watts delivered to a load. It is the only useful power. It is the actual power dissipated by the load. The reactive power Q is a measure of the energy exchange between the source and the reactive part of the load.

The unit of Q is the volt-ampere reactive (VAR) to distinguish it from the real power, whose unit is the watt.

Notice that:

1. Q = 0 for resistive loads (unity pf)
2. Q < 0 for capacitive loads (leading pf)
3. Q > 0 for inductive loads (lagging pf)

Thus,
Complex power (in VA) is the product of the rms voltage phasor and the complex conjugate of the rms current phasor. As a complex quantity, its real part is real power P and its imaginary part is reactive power Q.

Introducing the complex power enables us to obtain the real and reactive powers directly from voltage and current phasors.

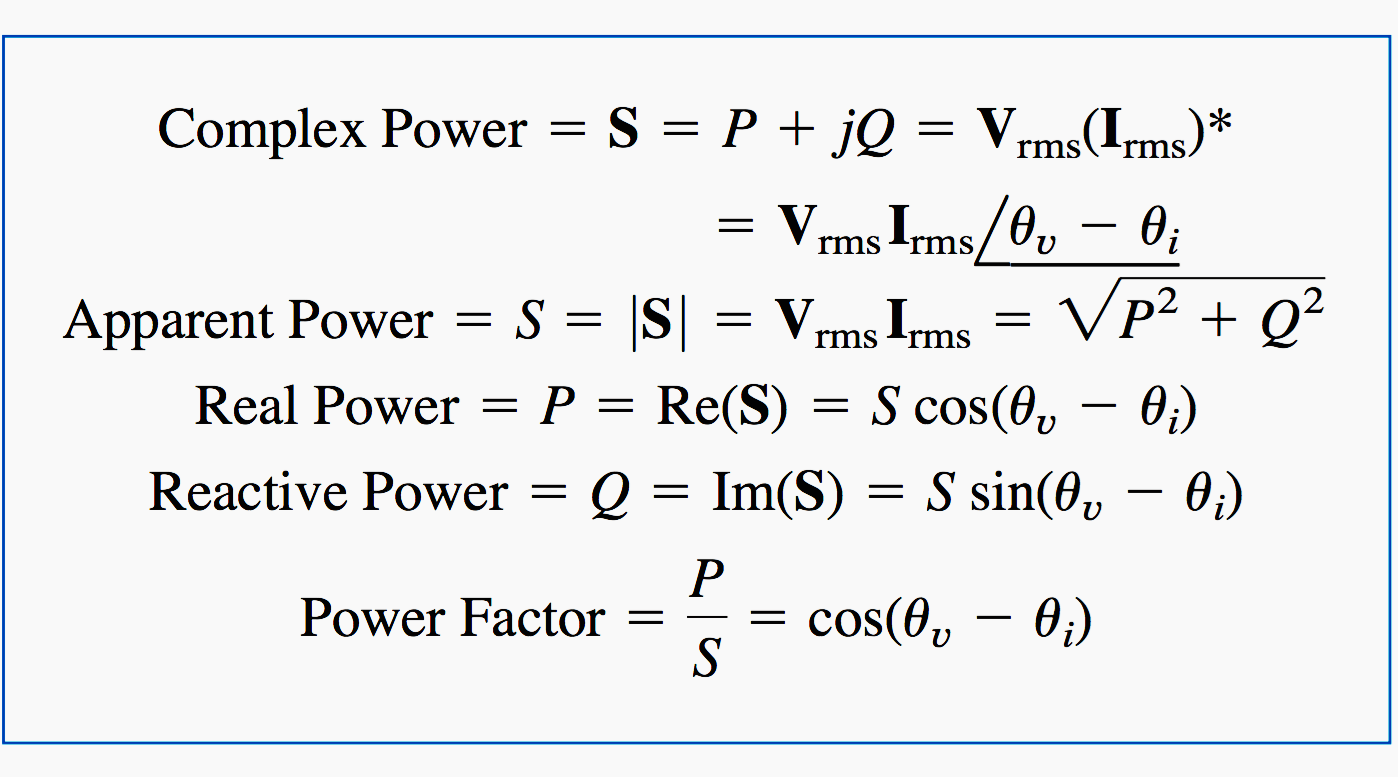
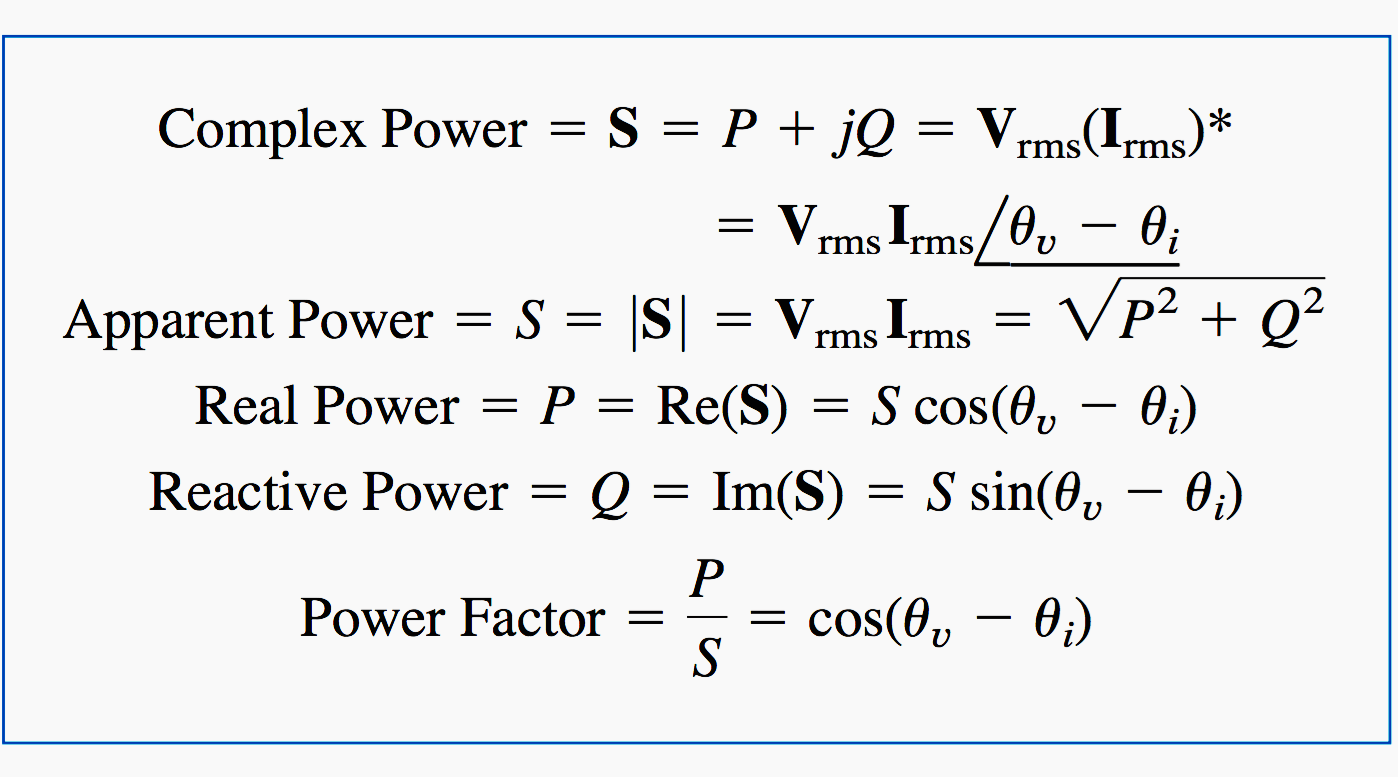
(1.21)

This shows how the complex power contains all the relevant power information in a given load.

It is a standard practice to represent S, P, and Q in the form of a triangle, known as the power triangle, shown in Fig. 2(a). This is similar to the impedance triangle showing the relationship between Z, R, and X, illustrated in Fig. 2(b).

S contains all power information of a load. The real part of S is the real power P. Its imaginary part is the reactive power Q. Its magnitude is the apparent power S. And the cosine of its phase angle is the power factor PF.

The power triangle has four items:

1. Apparent/complex power,
2. Real power,
3. Reactive power, and
4. Power factor angle.

Given two of these items, the other two can easily be obtained from the triangle.

As shown in Figure 3, when S lies in the first quadrant, we have an inductive load and a lagging PF. When S lies in the fourth quadrant, the load is capacitive and the PF is leading. It is also possible for the complex power to lie in the second or third quadrant.

This requires that the load impedance have a negative resistance, which is possible with active circuits.

Example with complex power calculations

Examples on complex power, power factor, average power and apparent power

Reference // Fundamentals of electric circuits by Charles K. Alexander and Matthew N. O. Sadiku (Purchase hardcopy form Amazon)