Fundamental overcurrent, distance and differential protection principles

Essential protection principles

The aim of this technical article is to cover the most important principles of four fundamental relay protections: overcurrent, directional overcurrent, distance and differential for transmission lines, power transformers and busbars.

Contents:

1. Principle of overcurrent protection
2. Principle of directional overcurrent protection
3. Principle of distance protection
4. Principle of differential protection
   1. For transmission line
   2. For transformer
   3. For busbar

For simplicity in explaining the key ideas, we consider three phase bolted faults.

1. Overcurrent protection

Transmission and distribution systems are susceptible to overcurrent flow within their components. In an electric power system, overcurrent refers to a condition when the electric current surpasses the intended level in a conductor, resulting in excessive heat generation and the potential for fire or equipment damage. Potential sources of overcurrent encompass short circuits, high load, transformer inrush current, motor initiation, design flaws, or ground faults.

Consequently, under standard system conditions, various strategies including demand-side management, load shedding, and gentle motor starting may be utilized to prevent overloads.

Moreover, distribution systems are outfitted with protective relays that activate mechanisms to ensure switching equipment responds solely to atypical system conditions.

This scheme is based on the intuition that, faults typically short circuits, lead to currents much above the load current. We can call them as overcurrents. Over current relaying and fuse protection uses the principle that when the current exceeds a predetermined value, it indicates presence of a fault (short circuit).

This protection scheme finds usage in radial distribution systems with a single source. It is quite simple to implement.

Figure 1 – Radial distribution system

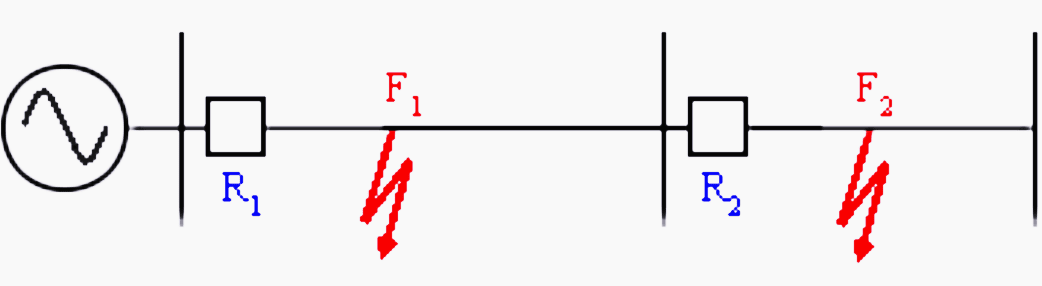
Figure 1 shows a radial distribution system with a single source. The fault current is fed from only one end of the feeder.

For this system it can be observed that:

• To relay R₁, both downstream faults F₁ and F₂ are visible i.e. I_F1 as well as I_F2 pass through CT of R₁.
• To relay R₂, fault F₁, an upstream fault is not seen, only F₂ is seen. This is because no component of I_F1 passes through CT of R₂. Thus, selectivity is achieved naturally.
  
  Relaying decision is based solely on the magnitude of fault current. Such a protection scheme is said to be non-directional.

Go back to protection principles ↑

2. Directional overcurrent protection

Ground distance and directional ground overcurrent relays are frequently employed to identify ground faults in transmission lines. Ground distance relays may lack sufficient sensitivity to identify all impedance-limited ground faults due to the limitations of the distance element characteristic on resistive reach.

Ground overcurrent relays are more adept at detecting these faults due to their superior sensitivity to resistance-limited faults.

The nature of grounding, system characteristics, and individual fault impedance dictate the severity of ground faults. Faults with considerable impedance exhibit a comparatively modest current magnitude compared to faults lacking significant impedance. Such faults can challenge distance relays because to their sensitivity related to the angle of the line characteristic impedance.

In contrast, there can be situations where for the purpose of selectivity, phase angle information (always relative to a reference phasor) may be required. Figure 2 shows such a case for a radial system with source at both ends. Consequently, fault is fed from both the ends of the feeder.

To interrupt the fault current, relays at both ends of the feeder are required.

Figure 2 – Radial system with source at both ends

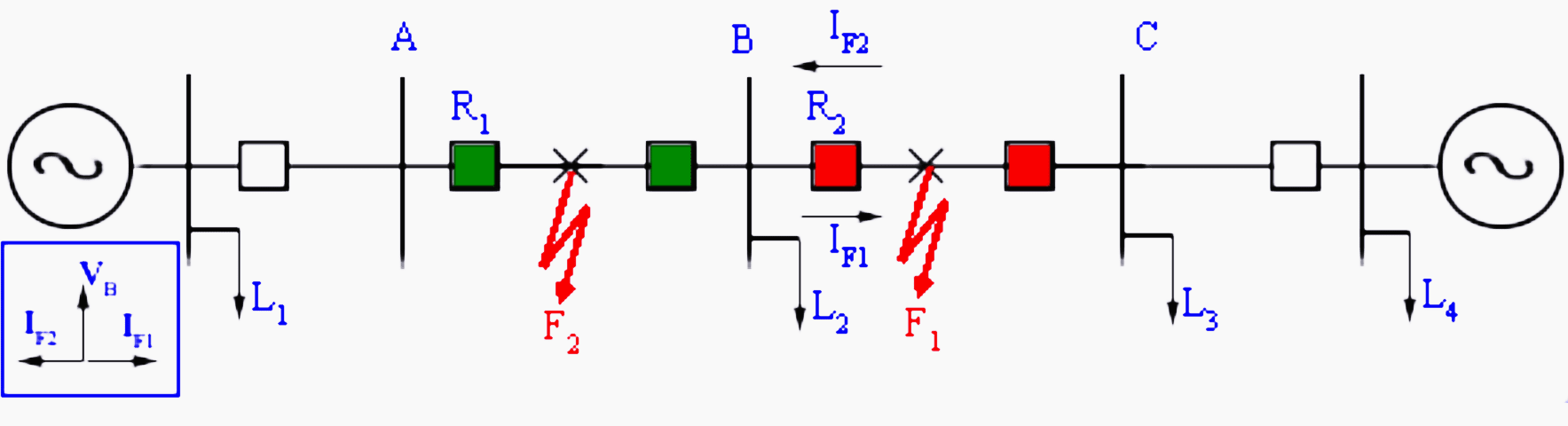
In this case, from the magnitude of the current seen by the relay R₂, it is not possible to distinguish whether the fault is in the section AB or BC. Since faults in section AB are not in its jurisdiction, it should not trip.

Go back to protection principles ↑

3. Distance protection

Distance relaying should be implemented when overcurrent relaying is insufficiently fast or lacks selectivity. Distance relays are typically employed for primary and backup protection against phase faults on subtransmission lines, as well as on transmission lines where high-speed automated reclosing is unnecessary for stability and where a brief delay for end-zone faults is acceptable

Overcurrent relays have traditionally been employed for primary and backup protection against ground faults; however, there is an increasing inclination towards utilizing distance relays for ground fault protection as well.

Single-step distance relays are employed for phase-fault backup protection at generator terminals. Single-step distance relays may be beneficial for backup protection at power transformer banks; however, current practice typically use inverse-time overcurrent relays for this purpose.

Consider a simple radial system, which is fed from a single source. Let us measure the apparent impedance (V/I) at the sending end.

For the unloaded system, I = 0, and the apparent impedance seen by the relay is infinite. As the system is loaded, the apparent impedance reduces to some finite value (Z_L+Z_line) where Z_L is the load impedance and Z_line is the line impedance. In presence of a fault at a per-unit distance ‘m’, the impedance seen by the relay drops to a mZ_line as shown in figure 3 below.

Figure 3 – Fault in transmission line

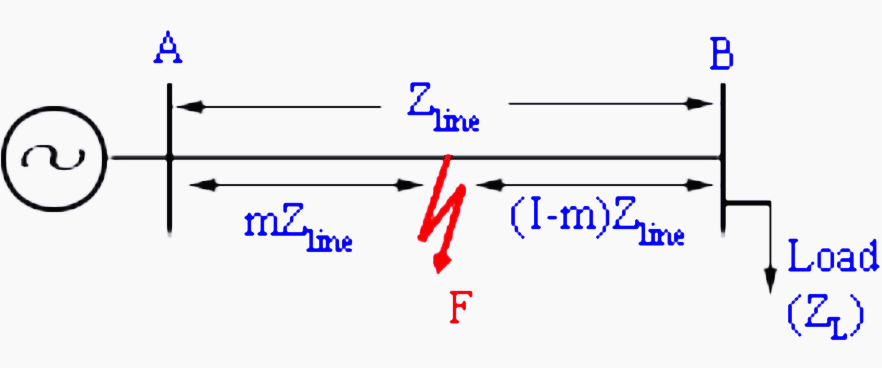
The basic principle of distance relay is that the apparent impedance seen by the relay, which is defined as the ratio of phase voltage to line current of a transmission line (Z_app), reduces drastically in the presence of a line fault. A distance relay compares this ratio with the positive sequence impedance (Z₁) of the transmission line. If the fraction Z_app/Z₁ is less than unity, it indicates a fault. This ratio also indicates the distance of the fault from the relay.

However, if only magnitude information is used, non-directional impedance relay results. Figures 4 and 5 shows a characteristic of an impedance relay and ‘mho relay’ both belonging to this class.

Figures 4, 5 – Figure 4 (left) – Impedance relay; Figure 5 (right) – Mho relay

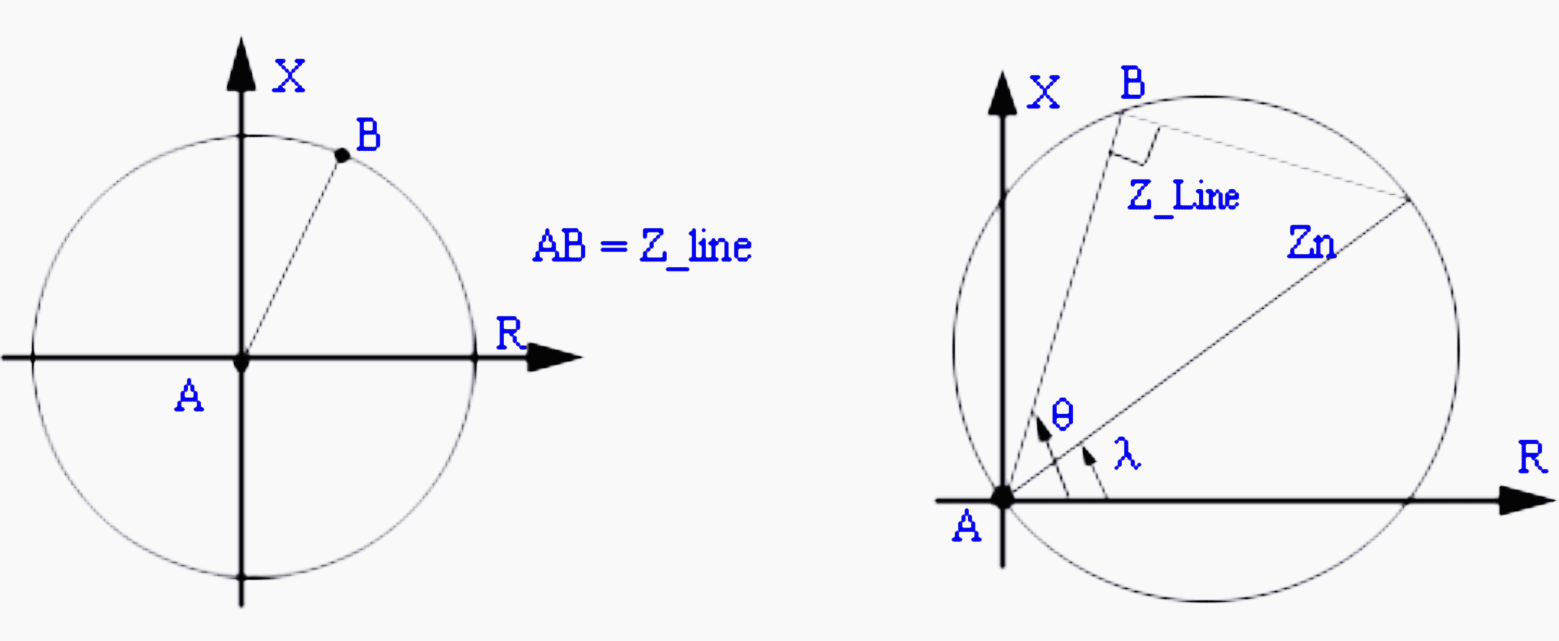
The impedance relay trips if the magnitude of the impedance is within the circular region. Since, the circle spans all the quadrants, it leads to non-directional protection scheme. In contrast, the mho relay which covers primarily the first quadrant is directional in nature.

Thus, the trip law for the impedance relay can be written as follows:

|Z_app| = |V_R| / |I_R| < |Z_set|

then trip; else restrain.

While impedance relay has only one design parameter, Z_set; ‘mho relay’ has two design parameters Z_n, λ. The trip law for mho relay is given by if:

|Z_app| < |Z_n| cos (θ – λ)

then trip; else restrain.

Go back to protection principles ↑

4. Principle of differential protection

Differential protection is based on the fact that any fault within an electrical equipment would cause the current entering it, to be different, from the current leaving it. Thus by comparing the two currents either in magnitude or in phase or both we can determine a fault and issue a trip decision if the difference exceeds a predetermined set value.

Figure 6 – Differential protection of short transmission line

Go back to protection principles ↑

4.1 Differential protection for transmission line

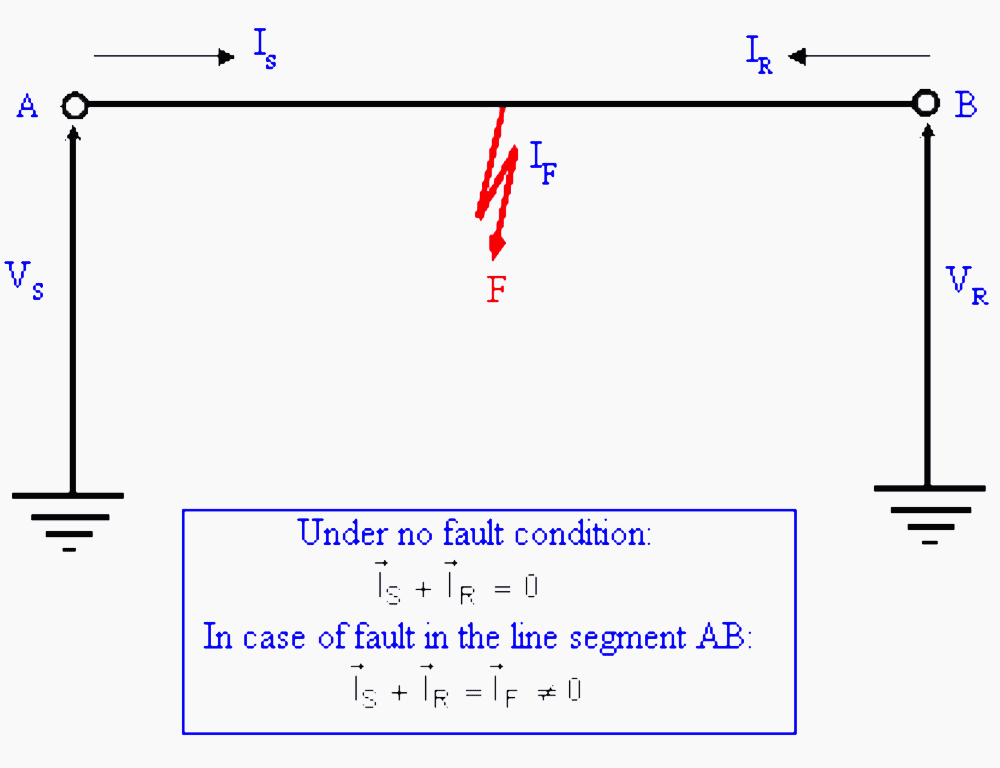
Figure 6 shows a short transmission line in which shunt charging can be neglected. Then under no fault condition, phasor sum of currents entering the device is zero i.e.

I_S + I_R = 0

Thus, we can say that differential current under no fault condition is zero. However in case of fault in the line segment AB, we get:

I_S + I_R = I_F ≠ 0

i.e. differential current in presence of fault is non-zero.

In case of transmission line, implementation of differential protection requires a communication channel to transmit current values to the other end. It can be used for short feeders and a specific implementation is known as pilot wire protection. Differential protection tends to be extremely accurate. Its zone is clearly demarcated by the CTs which provide the boundary.

Differential protection can be used for tapped lines (multiterminal lines) where boundary conditions are defined as follows:

Figure 7 – Differential protection for tapped transmission line

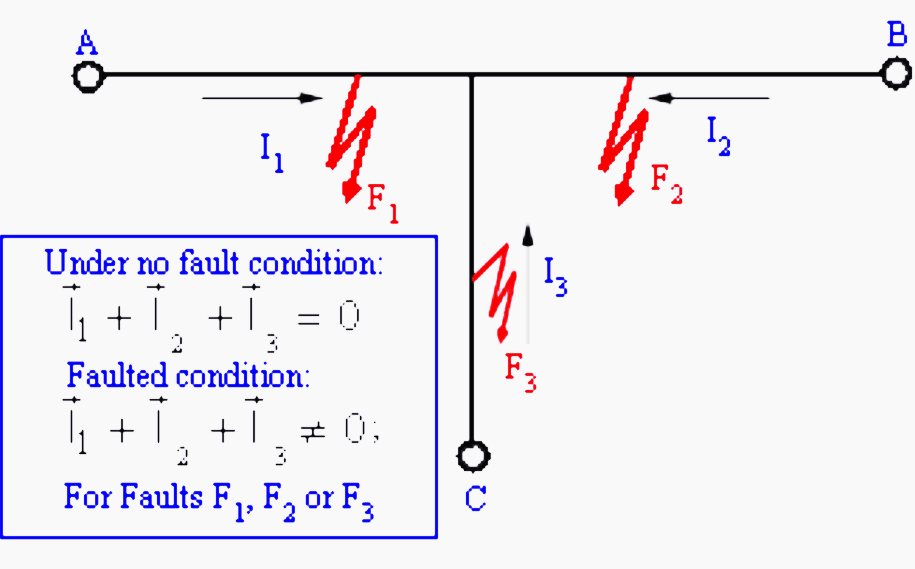
Under no fault condition:

I₁ + I₂ + I₃ = 0

Faulted condition:

I₁ + I₂ + I₃ ≠ 0

Go back to protection principles ↑

4.2 Differential protection for transformer

Differential protection for detecting faults is an attractive option when both ends of the apparatus are physically located near each other. e.g. on a transformer, a generator or a bus bar.

Consider an ideal transformer with the CT connections, as shown in Figure 8.

Figure 8 – Differential protection for transformer

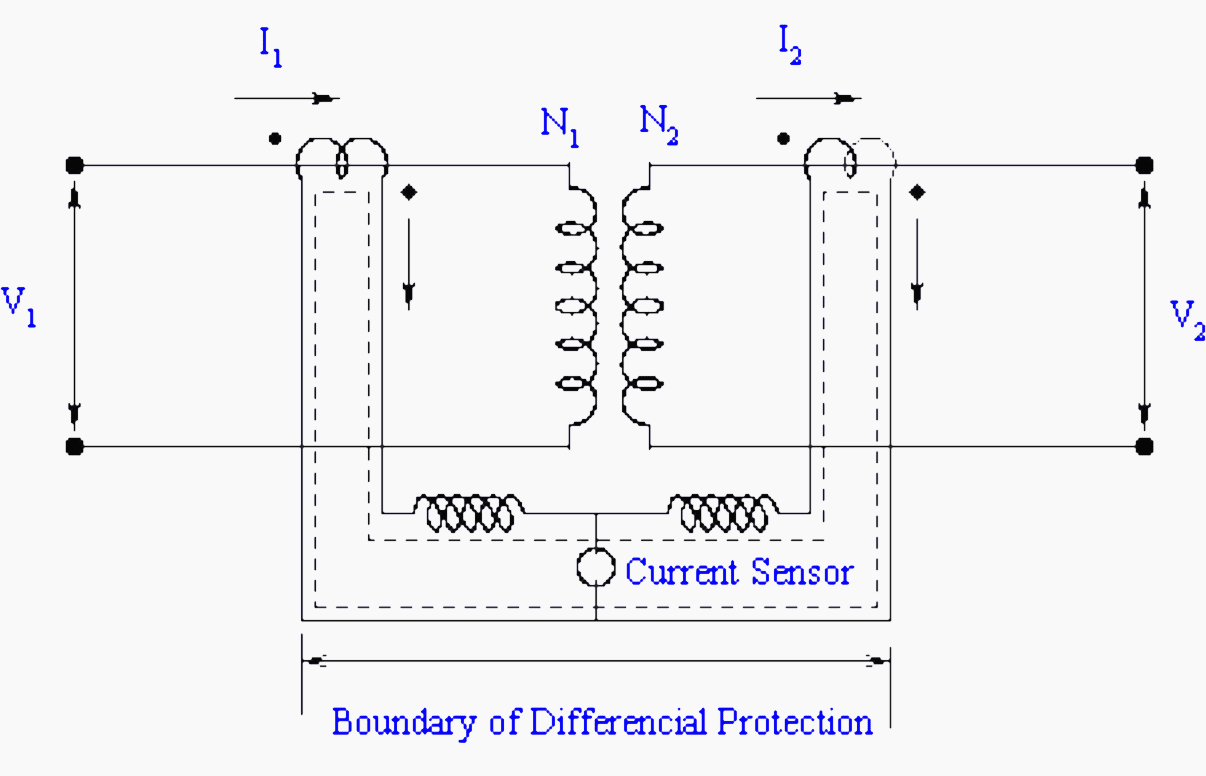
To illustrate the principle let us consider that current rating of primary winding is 100A and secondary winding is 1000A. Then if we use 100:5 and 1000:5 CT on the primary and secondary winding, then under normal (no fault) operating conditions the scaled CT currents will match in magnitudes. By connections the primary and secondary CTs with due care to the dots (polarity markings), a circulating current can be set up as shown by dotted line.

Now if an internal fault occurs within the device like interturn short etc., then the normal mmf balance is upset i.e. N₁I₁ ≠ N₂I₂. Under this condition, the CT secondary currents of primary and secondary side CTs will not match. The resulting differential current will flow through overcurrent relay. If the pick up setting of overcurrent relay is close to zero, it will immediately pick up and initiate the trip decision.

In practice, the transformer is not ideal. Consequently, even if I₂=0, I₁≠0, it is the magnetization current or (no load) current. Thus, a differential current always flows through the overcurrent relay.

Therefore overcurrent relay pick up is adjusted above the no load current value. Consequently, minute faults below no load current value cannot be detected. This compromises sensitivity.

Go back to protection principles ↑

4.3 Differential protection for busbar

Ideally, differential protection is the solution for the busbar protection. Figure 9 illustrates the basic idea. If the fault is external to the bus, it can be seen that algebraic sum of the currents entering the bus is zero.

I_A + I_B + I_C + I_D + I_E = 0

Figure 9 – Differential protection for busbar

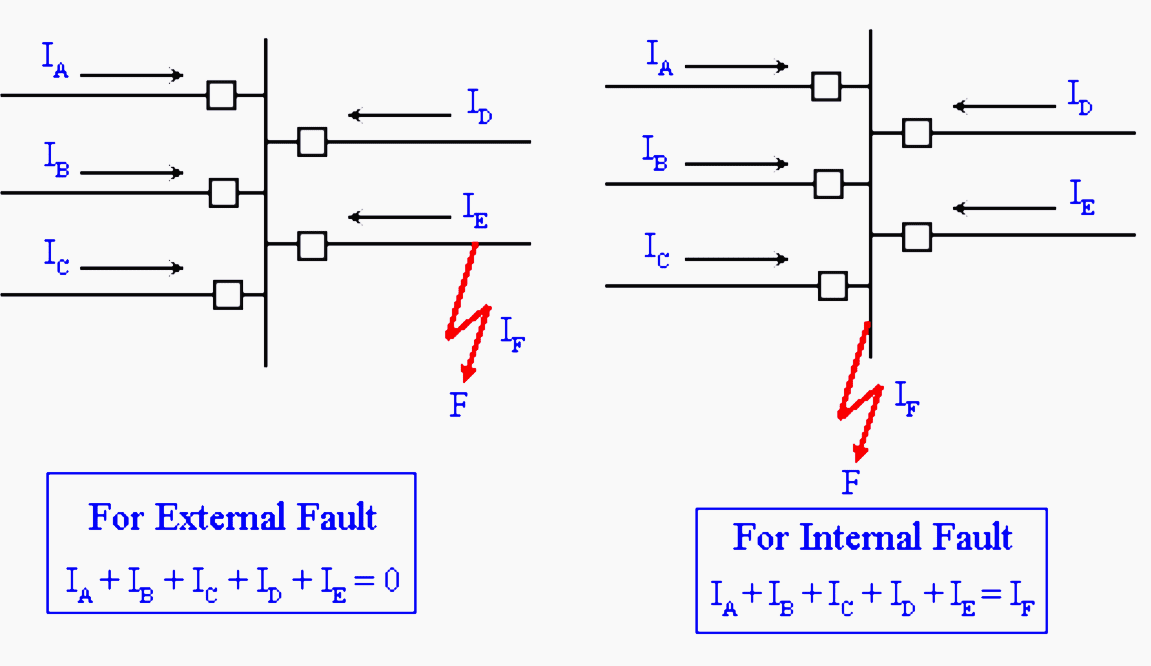
On the other hand, if fault is on the bus (internal fault), this sum is not zero.

I_A + I_B + I_C + I_D + I_E = I_F

Thus, differential protection can be used to protect a bus.

Go back to protection principles ↑

Reference: Fundamentals of Power System Protection – Extract from IIT Bombay NPTEL