Delta-Star Transformation

To convert a delta network to an equivalent star network we need to derive a transformation formula for equating the various resistors to each other between the various terminals. Consider the circuit below.

Delta to Star Network.

Compare the resistances between terminals 1 and 2.

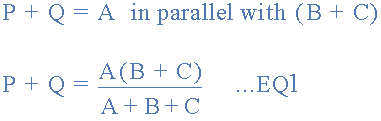
Resistance between the terminals 2 and 3.

Resistance between the terminals 1 and 3.

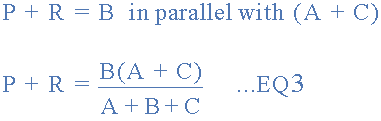
This now gives us three equations and taking equation 3 from equation 2 gives:

Then, re-writing Equation 1 will give us:

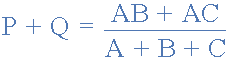
Adding together equation 1 and the result above of equation 3 minus equation 2 gives:

From which gives us the final equation for resistor P as:

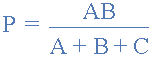
Then to summarize a little the above maths, we can now say that resistor P in a Star network can be found as Equation 1 plus (Equation 3 minus Equation 2) or   Eq1 + (Eq3 – Eq2).

Similarly, to find resistor Q in a star network, is equation 2 plus the result of equation 1 minus equation 3 or  Eq2 + (Eq1 – Eq3) and this gives us the transformation of Q as:

and again, to find resistor R in a Star network, is equation 3 plus the result of equation 2 minus equation 1 or  Eq3 + (Eq2 – Eq1) and this gives us the transformation of R as:

When converting a delta network into a star network the denominators of all of the transformation formulas are the same: A + B + C, and which is the sum of ALL the delta resistances. Then to convert any delta connected network to an equivalent star network we can summarized the above transformation equations as:

Delta to Star Transformations Equations

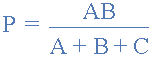
Example No1

Convert the following Delta Resistive Network into an equivalent Star Network.

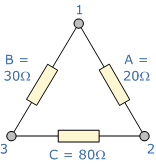
Star Delta Transformation

We have seen above that when converting from a delta network to an equivalent star network that the resistor connected to one terminal is the product of the two delta resistances connected to the same terminal, for example resistor P is the product of resistors A and B connected to terminal 1. By rewriting the previous formulas a little we can also find the transformation formulas for converting a resistive star network to an equivalent delta network giving us a way of producing a star delta transformation as shown below.

Star to Delta Network.

The value of the resistor on any one side of the delta, Δ network is the sum of all the two-product combinations of resistors in the star network divide by the star resistor located “directly opposite” the delta resistor being found. For example, resistor A is given as:

with respect to terminal 3 and resistor B is given as:

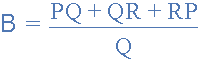
with respect to terminal 2 with resistor C given as:

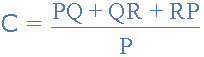
with respect to terminal 1.

By dividing out each equation by the value of the denominator we end up with three separate transformation formulas that can be used to convert any Delta resistive network into an equivalent star network as given below.

Star Delta Transformation Equations

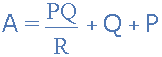
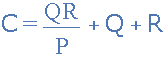
One final point about converting a star resistive network to an equivalent delta network. If all the resistors in the star network are equal in value then the resultant resistors in the equivalent delta network will be three times the value of the star resistors and equal, giving:   R_DELTA = 3R_STAR

Reference: Electronics Tutorials