85% of energy lost as waste heat…
Instrumentation consumes large amounts of compressed air at many individual locations in a textile plant, but these uses are susceptible to leakage. Most such leaks are at threaded connection points, rubber hose connections, valves, regulators, seals, and in old pneumatic equipment.

Air leaks from knitting operations are very common and can be quite large; these exact a large invisible cost, and the reduced pressure may impair the operation of the dyeing and finishing machines. Integrated mills that contain knitting operations should check the compressed air systems in knitting as well as in the dyeing and finishing areas.
Many opportunities exist to reduce energy use of compressed air systems. For optimal savings and performance, it is recommended that a systems approach is used.
An example of compressed air plant diagram (click to expand):
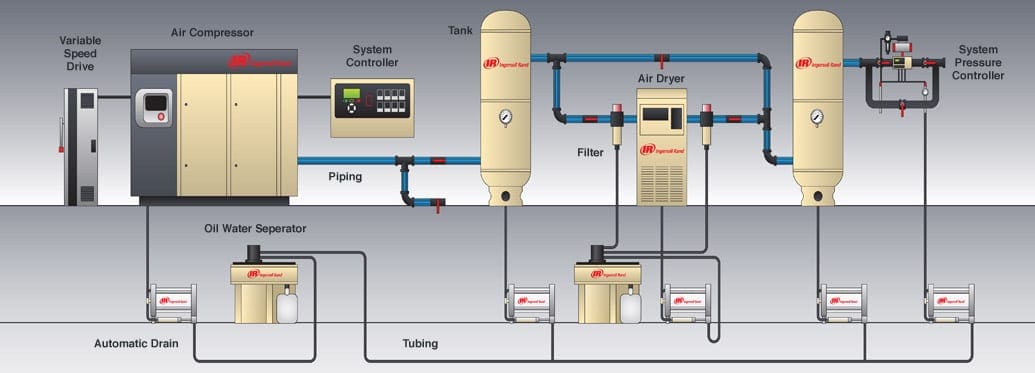

In the following, energy saving opportunities for compressed air systems are presented.
Also, Energy Assessment for Compressed Air Systems (ASME) has published a standard that covers the assessment of compressed air systems that are defined as a group of subsystems of integrated sets of components for consistent, reliable, and efficient use of energy. In this standard the procedure of conducting a detailed energy assessment of the compressed air system as well as the energy efficiency opportunities are described.
- Reduction of demand
- Maintenance
- Monitoring
- Reduction of leaks (in pipes and equipment)
- Electronic condensate drain traps (ECDTs)
- Reduction of the inlet air temperature
- Maximizing allowable pressure dew point at air intake
- Optimizing the compressor to match its load
- Proper pipe sizing
- Heat recovery
- Installing adjustable speed drives (ASDs)
1. Reduction of demand
Because of the relatively expensive operating costs of compressed air systems, the minimum quantity of compressed air should be used for the shortest possible time, constantly monitored and reweighed against alternatives.
2. Maintenance
Inadequate maintenance can lower compression efficiency, increase air leakage or pressure variability and lead to increased operating temperatures, poor moisture control and excessive contamination. Better maintenance will reduce these problems and save energy.


3. Monitoring
Maintenance can be supported by monitoring using proper instrumentation, including following:
- Pressure gauges on each receiver or main branch line and differential gauges across dryers, filters, etc.
- Temperature gauges across the compressor and its cooling system to detect fouling and blockages.
- Flow meters to measure the quantity of air used.
- Dew point temperature gauges to monitor the effectiveness of air dryers.
- kWh meters and hours run meters on the compressor drive.


4. Reduction of leaks (in pipes and equipment)
Leaks cause an increase in compressor energy and maintenance costs. The most common areas for leaks are:
- Couplings,
- Hoses,
- Tubes,
- Fittings,
- Pressure regulators,
- Open condensate traps and shut-off valves,
- Pipe joints,
- Disconnects and
- Thread sealants.
Quick connect fittings always leak and should be avoided.
In addition to increased energy consumption, leaks can make pneumatic systems/equipment less efficient and adversely affect production, shorten the life of equipment, lead to additional maintenance requirements and increased unscheduled downtime.
A simple way to detect large leaks is to apply soapy water to suspect areas. The best way is to use an ultrasonic acoustic detector, which can recognize the high frequency hissing sounds associated with air leaks.


5. Electronic condensate drain traps (ECDTs)
Due to the necessity to remove condensate from the system, continuous bleeding, achieved by forcing a receiver drain valve to open, often becomes the normal operating practice, but is extremely wasteful and costly in terms of air leakage.
The payback period depends on the amount of leakage reduced, and is determined by the pressure, operating hours, the physical size of the leak and electricity costs.


6. Reduction of the inlet air temperature
Reducing the inlet air temperature reduces energy used by the compressor. In many plants, it is possible to reduce this inlet air temperature by taking suction from outside the building. Importing fresh air has paybacks of up to 5 years, depending on the location of the compressor air inlet.
As a rule of thumb, each 3°C reduction will save 1% compressor energy use (CADDET, 1997; Parekh, 2000).
7. Maximizing allowable pressure dew point at air intake
Choose the dryer that has the maximum allowable pressure dew point, and best efficiency. A rule of thumb is that desiccant dryers consume 7 to 14% and refrigerated dryers consume 1 to 2% of the total energy of the compressor.
Consider using a dryer with a floating dew point. Note that where pneumatic lines are exposed to freezing conditions, refrigerated dryers are not an option.


8. Optimizing the compressor to match its load
Plant personnel have a tendency to purchase larger equipment than needed (that’s true indeed), driven by safety margins or anticipated additional future capacity. Given the fact that compressors consume more energy during part-load operation, this is something that should be avoided.
In some cases, the pressure required is so low that the need can be met by a blower instead of a compressor which allows considerable energy savings, since a blower requires only a small fraction of the power needed by a compressor.


9. Proper pipe sizing
Pipes must be sized correctly for optimal performance or resized to fit the compressor system. Inadequate pipe sizing can cause pressure losses, increase leaks and increase generating costs. Increasing pipe diameter typically reduces annual compressor energy consumption by 3%.


10. Heat recovery
As mentioned at the beginning of article, more than 85% of the electrical energy used by an industrial air compressor is converted into heat. A 150 hp compressor can reject as much heat as a 90 kW electric resistance heater or a 422 MJ/hour natural gas heater when operating.
With large water-cooled compressors, recovery efficiencies of 50 to 60% are typical. When used for space heating, the recovered heat amount to 20% of the energy used in compressed air systems annually.
Paybacks are typically less than one year.
In some cases, compressed air is cooled considerably below its dew point in refrigerated dryers to condense and remove the water vapor in the air. The waste heat from these aftercoolers can be regenerated and used for space heating, feedwater heating or process-related heating.


11. Installing adjustable speed drives (ASDs)
When there are strong variations in load and/or ambient temperatures there will be large swings in compressor load and efficiency. In those cases installing an ASD may result in attractive payback periods.
Implementing adjustable speed drives in rotary compressor systems has saved 15% of the annual compressed air system energy consumption.


Reference // Industrial Energy Audit Guidebook: Guidelines for Conducting an Energy Audit in Industrial Facilities – Ali Hasanbeigi, Lynn Price











isn’t air dryer compressor is a big impact of saving cost of 2tons boiler unit? which include saving cost of steam flow to reduce the fuel cost of boiler?
Thanks!
Thanks!
Very helpful information, Thank you.
thanks Edward. its a nice article
Thank you Edvard it’s useful for energy save
thanks a lot Mr Edvard
all your articles are very nice and useful
Nice, Useful & true articales for energy conservation programme