
Understanding power factor is not that hard. We have some very common example from the real life you will understand for sure, but first let’s start with some introduction of power factor.
To understand power factor, we’ll first start with the definition of some basic terms:
kW is Working Power (also called Actual Power or Active Power or Real Power). It is the power that actually powers the equipment and performs useful work.
kVAR is Reactive Power. It is the power that magnetic equipment (transformer, motor, relay etc.) needs to produce the magnetizing flux.
kVA is Apparent Power. It is the “vectorial summation” of KVAR and KW.
Example From the Real Life ;)

Let’s look at a simple analogy in order to better understand these terms….
Let’s say it’s friday evening, and you are with your friends at your favorite pub after really hot day. You order up a big mug of your favorite beer for you and for your friends. The thirst-quenching portion of your beer is represented by KW (the big pic on top).
The total contents of your mug, KVA, is this summation of KW (the beer) and KVAR (the foam).
So, now that we understand some basic terms, we are ready to learn about power factor:
Power Factor (P.F.) is the ratio of Working Power to Apparent Power.
![]()
Looking at our beer mug analogy above, power factor would be the ratio of beer (KW) to beer plus foam (KVA).
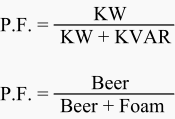
Thus, for a given KVA:
- The more foam you have (the higher the percentage of KVAR), the lower your ratio of KW (beer) to KVA (beer plus foam). Thus, the lower your power factor.
- The less foam you have (the lower the percentage of KVAR), the higher your ratio of KW (beer) to KVA (beer plus foam). In fact, as your foam (or KVAR) approaches zero, your power factor approaches 1.0.
Our beer mug analogy is a bit simplistic. In reality, when we calculate KVA, we must determine the “vectorial summation” of KVAR and KW. Therefore, we must go one step further and look at the angle between these vectors.
Power Triangle
The “Power Triangle” illustrates this relationship between KW, KVA, KVAR, and Power Factor:

Note that in an ideal world looking at the beer mug analogy:
- KVAR would be very small (foam would be approaching zero)
- KW and KVA would be almost equal (more beer; less foam)
There are dosen of tools and technical articles/guides published at EEP that can help you to understand power factor and its controlling. Hope these can help:
- Power Factor Correction Calculation (MS Excel Spreadsheet)
- Size of Capacitor For Power Factor Improvements
- How Power Factor Corection Works
- Capacitor Banks In Power System
- Economic advantages of power factor correction
Resource: powerstudies.com











I’m trying to use the power triangle to “do some beer math” but I am not getting the same answer. Using “beer math” (If KVA =300 Kw = 270 & PF= .9) my Kvar should be 30kw. Using the power triangle however, Kvar = √(300²-270²) which happens to equal 130.7 kvar. So I’m wondering what I’m missing because Kvar in beer math =30 but using the power triangle Kvar = 130. Help please, examples on this page would be helpful to explain finding a solution for Kvar/Kw/Kva would make understanding much easier. Thank you!
Beer glass analogy will impart wrong concept among the students as real power is vector sum of active power and reactive power but, beer glass analogy suggests real power as algebraic sum of active power and reactive power.Requesting to delete beer glass analogy to describe the power factor.
We have 2000KVAR shunt capacitor
We need to convert KW kindly workout formula and share me to given mail ID
33KV supply
HT current 75Amps
Thank you for the simplest explanation and beer analogy to help me understand P.F. As a non electrical engineer, this is a very handy information.
Thanks for the simple and easy explanation by the author and by the corrections by readers.
Man, there is a Mistake. PF with the sin is kw/kva=cos(Θ)=sin(90°-Θ)
The p.f. shown here with sin is indeed correct. SinΘ = perp/hyp = KVAR/KVA
What a great way to describe and explain the power factor. I like this style of learning.
The correct unit for reactive power is kvar, not kVAr.
No, actually its kVAr not kvar
Well said,good job
Very clear answer . Thank you
good
Instructions unclear. Beer now empty.
It is amazing how this how often this graphic turns up when you need to discuss reactive power and explain how it can affect electricity bills. With the ESOS deadline on the horizon it is even more relevant.
been using this way to explain kva and real power since the mid 90’s.
I would like to ask what is the appropriate KW rating of a generator set to used for 5 tonner aircondioning unit? Thanks
this is so simple and interesting. examples are just from day to day life.
Am student and iwant to know the way of achive my goal to be a engineer .
VERY EDUCATIVE
Excelente analogía. Interesante el portal
I didn’t see like this example wow its very help full
Analogy of Kirchoffs law
Dear Sir,Greetings.
Its a really interesting Practical Example.
Congrants for \an \idea.
Greatest description ever! ;) Thanks..
Very good example
Good Illustration. Hope people donot forget after having a beer. Cheers
merci d’un million de… Really appreciate this example……..
Jelen Beer FTW.
Srsly guys, you could’ve picked some less catastrophic Serbian beer :D
Palindrome: Jelenovi pivo nelej.
Excellent example, served me to explain the power factor to my clients.
We need more examples applicable to real life. Thanks
Is it correct to say that the equipment itself ‘eats’ a bit of the electricity that can be generated? So there is always a bit of loss in the generation process, lost to the equipment itself? Thanks much for this helpful article!
Great job….I love your power factor analogy using beer as an example!!!
i need more very common example from the real life like this.
Good approach to teach a topic in a simple way.
Great article I will never be able to look at me beers the same way again.
Took into this extent, the PUB is the Substation and the Brewerei is the Power Plant.
Good article. Easy to read and great analogy. However, the equation P.F. = KW/(KW + KVAR) needs to be corrected to P.F. = KW/(KW^2 + KVAR^2)^(1/2) since KVA=(KW^2 + KVAR^2)^(1/2). I understand how the author wanted to keep it simple by associating his beer equation (P.F.= Beer/(Beer + Foam) ) with the actual power factor equation, but this is misleading and will lead to errors. People who aren’t comfortable with this topic will use P.F. = KW/(KW + KVAR) and will not obtain a correct answer.
cool…. yesterday only i was questioned on this by laboratory viva examiner!! wish i read this before….