How capacitors improve the power factor and how to calculate them?

How to improve the power factor?

It’s quite simple. By installing capacitors or capacitor banks. Improving the power factor of an electrical installation consists of giving it the means to “produce” a certain proportion of the reactive energy it consumes itself.

The capacitor is most frequently used, given:

1. Its non-consumption of active energy
2. Its purchase cost
3. Its ease of use
4. Its service life (approximately 10 years)
5. Its low maintenance (static device)

Power diagram

Power factor is the ratio of working power to apparent power. It measures how effectively electrical power is being used.

To determine power factor (PF), divide working power (kW) by apparent power (kVA). In a linear or sinusoidal system, the result is also referred to as the cosine θ.

PF = kW / kVA = cosine θ kVA

For example, if you had a boring mill that was operating at 100 kW and the apparent power consumed was 125 kVA, you would divide 100 by 125 and come up with a power factor of 0.80.

(kW) 100 / (kVA) 125 = (PF ) 0.80

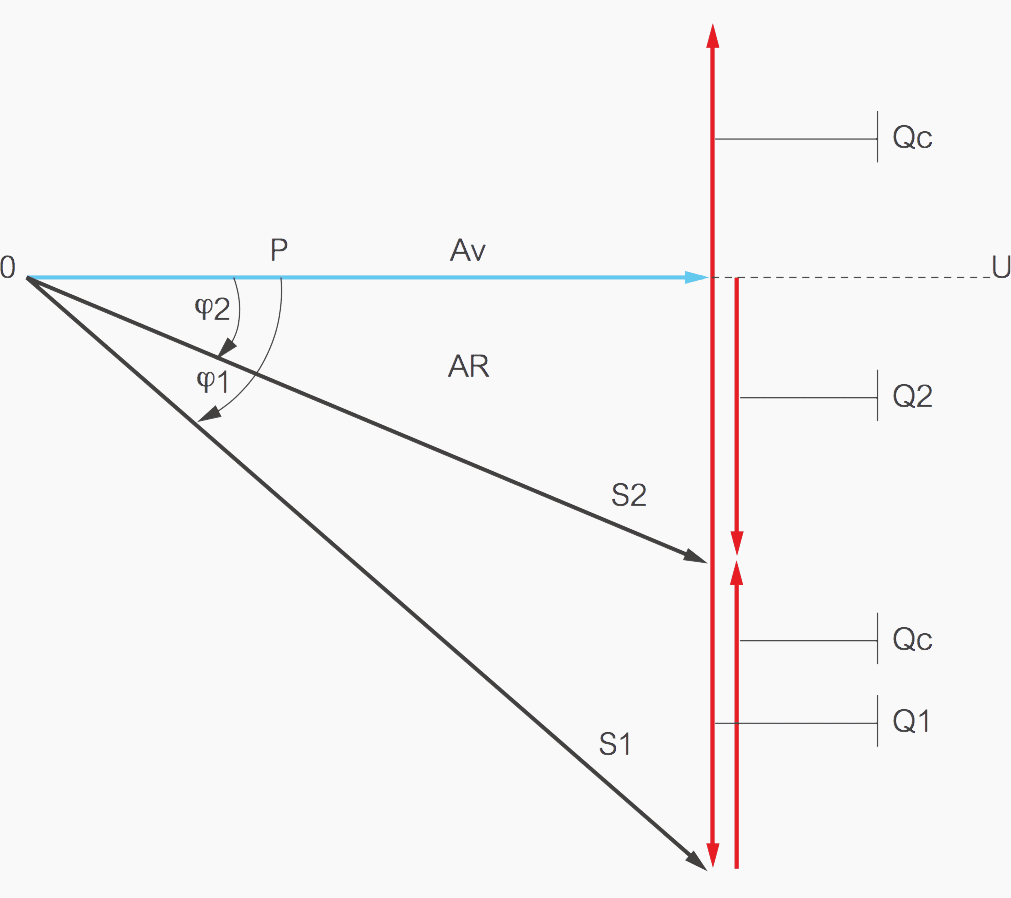
Where:

• P – Active power
• S1 and S2 – apparent powers
  (before and after compensation)
• Qc – capacitor reactive power
• Q1 – reactive power without capacitor Q2: reactive power with capacitor

Equations:

• Q2 = Q1 – Qc
• Qc = Q1 – Q2
• Qc = P×tg φ1 – P×tgφ2
• Qc = P×(tg φ1 – tg φ2)

Where φ1 is phase shift without capacitor and φ2 is phase shift with capacitor

The capacitor is a receiver composed of two conductive parts (electrodes) separated by an insulator. When this receiver is subjected to a sinusoidal voltage, the current and therefore its power (capacitive reactive) is leading the voltage by 90°.

Conversely, for all other receivers (motors, transformers, etc.) the current and therefore its power (reactive inductive) is lagging the voltage by 90°.

In simple terms, it is said that inductive receivers (motors, transformers, etc.) consume reactive energy whereas capacitors (capacitive receivers) produce reactive energy.

How to calculate the power of capacitors

Based on electricity bills to calculate the capacitor banks to be installed, use the following method:

• Select the month in which the bill is highest (kVArh to be billed)
• Assess the number of hours the installation operates each month
• Calculate the capacitor power Qc to be installed

Example for the subscriber //

• Highest reactive energy bill: December Number of kVArh to be billed: 70,000
• Monthly operating times: High-load + peak times = 350 hours

Qc (bank to be installed) = 70,000 / 350 = 200 kVAr

Based on measurements taken on the HV/LV transformer secondary: PkW-cosFI

Example //

An establishment supplied from an 800 KVA HV/LV subscriber station wanting to change the power factor of its installation to:

• Cosφ = 0.928 (tgφ = 0.4) at the primary
• I.e. Cosφ = 0.955 (tgφ = 0.31) at the secondary, with the following readings:
  • Voltage: 400 V 3-phase 50 HZ
  • PkW = 475
  • Cos (secondary) = 0.75 (i.e. tg ø = 0.88)

Qc (bank to be installed) = PkW x (tgφ measured – tgφ to be obtained)
Qc = 475 x (0.88 – 0.31) = 270 kVAr

Calculation for future installations:

Example

1000 kva transformer, Q capacitor = 250 kVAr

Note: This type of ratio corresponds to the following operating conditions:

• 1000 kVA transformer
• Actual transformer load = 75%
• Cosφ of the load = 0.80 } k = 0.421
• Cosφ to be obtained = 0.95 } – see table below

Qc = 1000 x 75% x 0.80 x 0.421 = 250 kVAr

Capacitor power calculation table

Conversion table

Based on the power of a receiver in kW, this table can be used to calculate the power of the capacitors to change from an initial power factor to a required power factor. It also gives the equivalence between cos ø and tg ø.

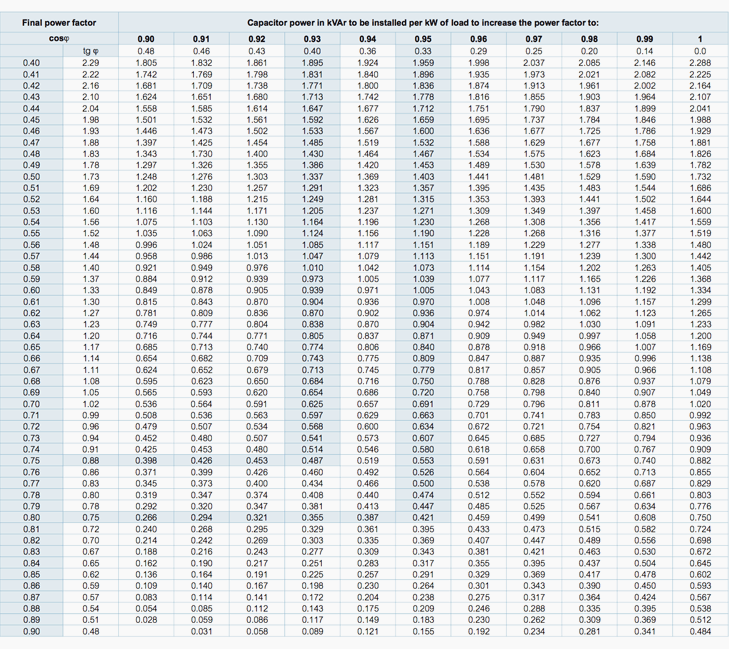
Example: 200 kW motor – cosφ = 0.75 – required cosφ = 0.93 – Qc = 200 x 0.487 = 98 kVAr

Reference // Reactive energy compensation and power quality monitoring by Legrand