Ungrounded systems
An ungrounded system is defined as a system of conductors with no intentional connection to ground except through potential indicating and/or measuring or other very high impedance devices.

This type of system is in reality coupled to ground through the distributed capacitance of conductors and transformer or motor phase windings.
In the absence of a ground fault the line-to-ground voltage of the three phases will be approximately equal because of the equally distributed capacitance of the system.
Effects of ground fault
Theoretically, in a balanced three-phase system, the currents in all three lines are equal and 120° apart (Figure 2.1(a)). The vector sum of the three capacitive phase currents (IA, IB and IC) is equal to zero at the ground point, which also results in the system neutral being held at ground potential by the balanced capacitive voltages to ground (VAG, VBG and VCG).
Thus, although an ungrounded system does not have an intentional connection to ground, the system is actually capacitively coupled to ground.
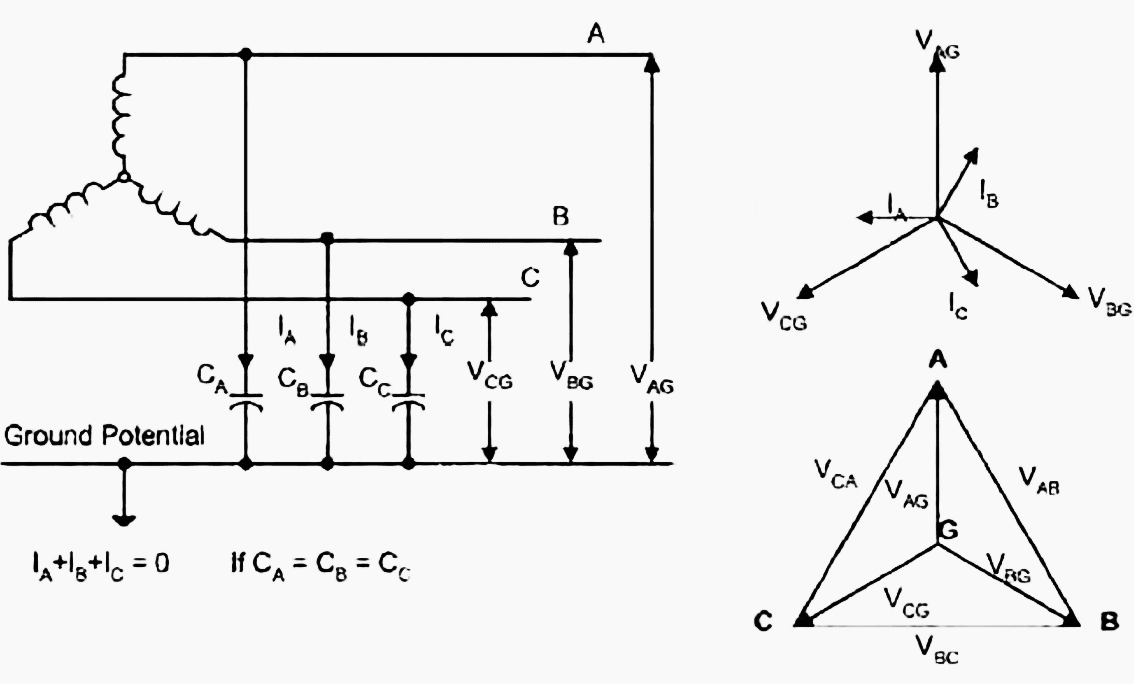
The ungrounded system can be regarded as a three-wire system only, thus the following discussion is valid for both wye and delta transformer secondaries.
If one system conductor, phase C for example, becomes faulted to ground, then phase C and ground are at the same potential, zero volts (Figure 2.1(b)). The voltages of the other two phases in the reference to ground are increased to the system phaseto-phase voltage.
This represents an increase of 73% over the normal line to ground voltage. Furthermore, the voltages to ground are now only 60° out of phase.
| Title: | Ground fault protection on ungrounded and high resistance grounded systems – Gard |
| Format: | |
| Size: | 947 kB |
| Pages: | 54 |
| Download: | Right here | Video Courses | Membership | Download Updates |



very usefull thanks