Concerns over electromagnetic fields below three-phase high voltage overhead lines

Electric and magnetic fields

In relation with the increased use of mobile phones during the last decades more concerns about possible harmful effects of electro-magnetic fields to human beings have been expressed. Overhead lines cause both electric and magnetic fields.

An important difference between the fields generated by antennas used for mobile communication and high voltage lines is the operating frequency. The fields of high voltage lines have a low frequency of 50 Hz, or 60 Hz, whereas the fields from antennas lie in the GHz domain.

Moreover, the very aim of antennas is the generation and radiation of fields whereas this is only an undesirable side effect in the case of high voltage lines.

Since we consider a symmetric three-phase system, the voltage in the single conductors are in each case phase-shifted by 120°, and the voltages and currents in the conductors vary with the power frequency of 50 Hz. These voltage and current variations influence the electromagnetic fields.

The field strength is dependent on the considered time instant, i.e. the fields are also alternating.

Let’s see now both electric and magnetic field of a high voltage line:

1. Electric Field
2. Magnetic Field

1. Electric Field

The electric field of a high voltage line depends on the voltage, the form of the tower and the configuration of the conductor lines. The analytic calculation of the electric field is very difficult because the earth impedance needs to be incorporated.

Hence, we abandon the derivation and present only the results of a simulation for the configuration given in Figure 1. In Figure 2 the behavior of the voltages of all three phases is shown. Regarding figure 1:

• u_R(t) corresponds to the voltage in the left conductor,
• u_S(t) to the one of the middle conductor and
• u_T(t) to the one in the right conductor.

In the following simulations three time instants t₁, t₂ and t₃ are considered, as indicated in Figure 2.

The resulting values of the electric fields are strongly dependent on the voltage. The electric field for phase to phase voltages of 110 kV, 220 kV and 400 kV (root mean square values) are considered. The electric field disappears exactly on the ground because the potential is zero there.

Related to the coordinate system in Figure 1, the values of the fields are shown in Figure 3 at a distance of 2 m above the ground, i.e. y = 2 m, up to 80 m in positive and negative x direction.

At the same time, the field assumes on average the maximal value (t₁) or the minimal value (t₂) at these time instants. The time instant t₃ is an example where the field is not symmetric.

As a comparison, the natural static air field obtains a field strength of around 0.1 kV/m. In connection with a thunderstorm, values up to 20 kV/m are possible.

Also in a house we are constantly exposed to electric fields from different appliances. Within a distance of 30 cm field strengths up to 0.5 kV/m can be measured around electric devices.

The values of electric fields which are generated by high voltage lines at 2 m above ground (Figure 3) are thus not much stronger than those we are exposed to from other sources.

Go back to contents ↑

2. Magnetic Field

In contrast with the electric field the magnetic field can be computed analytically quite easily as the earth influences the magnetic field only insignificantly.

Using the law of Biot-Savart, a straight current-carrying conductor creates a magnetic field with the value (formula 1):

Thereby R denotes the distance between the point at which the field is computed and the conductor, and the direction of the field is always tangential to the circles around the conductor.

This can now be applied for the calculation of the magnetic field for a three-phase line. For each conductor the value and the direction of the magnetic field is determined. Then, the three field vectors resulting of the three phases are summed up and the overall value of the field is computed.

As the field of a straight conductor only depends on the distance between the conductor and the point at which the field is computed (Formula 1), we can use a two-dimensional model to derive the formulas.

For a single conductor the relations are given in Figure 4.

The value of the magnetic field at location (x_B|h) results with (Formula 1) in:

Thereby we assume that I flows in the positive z direction, i.e. out from the paper. In opposite direction I becomes negative. In order to sum up the magnetic fields of all three phases, B is split into x and y coordinates:

With:

this results in:

The calculation of the overall field is carried out by summing up the single fields in the x and y directions. This field varies in time just as the electric field does.

In Figure 5 the root mean square (rms) values of the overall field for the configuration in Figure 1 and for the phase to phase rms currents of 1000 A, 700 A and 500 A at a distance of 2 m above the ground are given. (This means that the phase currents are these values divided by √3.)

It is assumed that the conductor height is constantly 20 m. Considering a line sag would result in higher values for the magnetic field.

The rms is calculated by the instantaneous values as follows:

The calculation of the magnetic field at large distances of the conductor can be simplified by some approximations.

As the direction of the magnetic field is always tangential to the circle around the conductor, we can conclude that the overall field is more or less perpendicular (normal) to earth at large distances (Figure 6).

We assume that the distance between P and the conductor corresponds to the distance in x direction, for example the distance for the conductor on the left hand side amounts to x + a.

In phasor notation the magnetic field at P results in:

With the approximation

for small ε this results in:

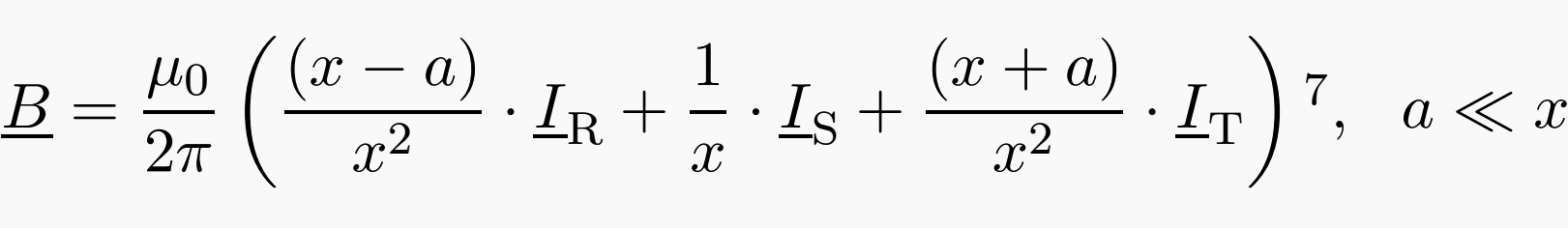
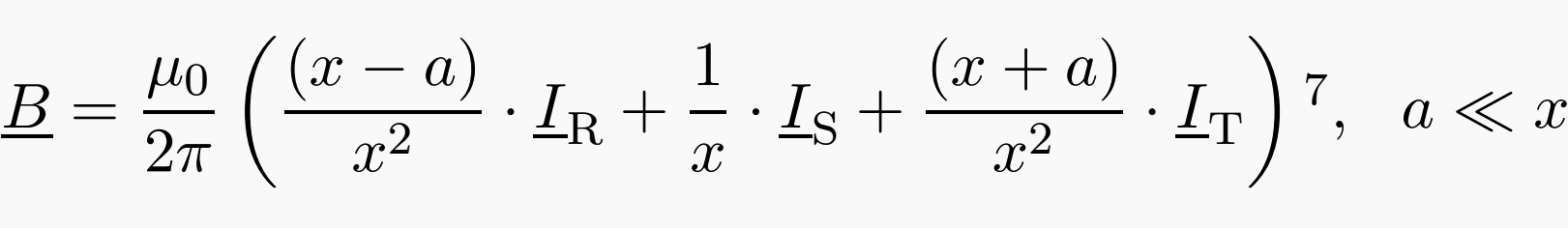
From the condition that the sum of the currents is equal to zero at each time instant:

the simple formula:

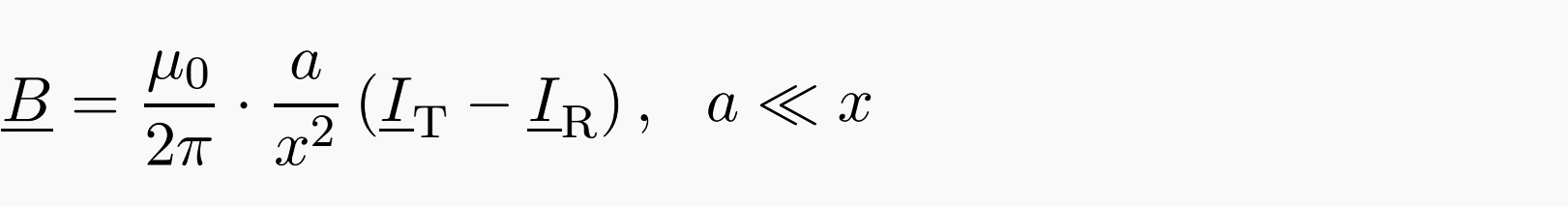
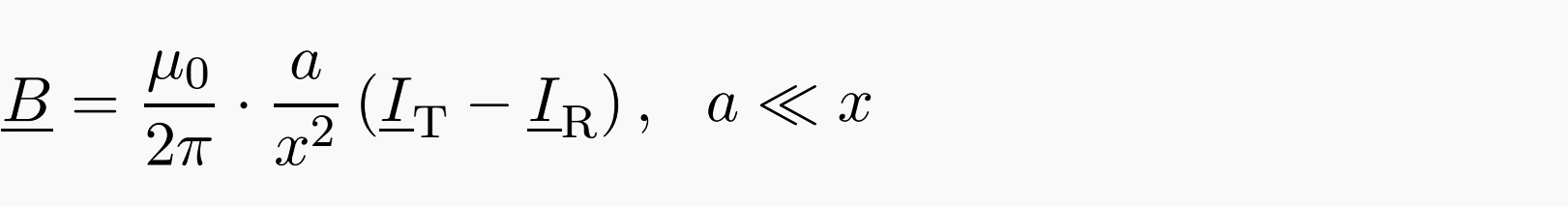
is derived, and therewith also the absolute value of the magnetic field at large distances (Formula 2):

Thereby I_ph denotes the phase current in A; with x and a in meter a flux density B in T results. For the calculation of the field directly below an overhead line, (formula 2) cannot be employed, because the assumption that the distance between the conductors is much smaller that the distance to the point of computation does not hold anymore.

Although magnetic fields are hardly damped by the human skin, they induce only small currents within the body.

Electric household devices, such as mixers or electric irons generate magnetic fields with amounts up to 10 µT at a distance of 30 cm. For causing heart problems for humans alternating field strengths at a frequency of 50 Hz and 1 Tesla are needed. This is ten thousand times more than the field strength below a high voltage line.

Although hundreds of research studies by scientists all over the world have concluded that no harm or damage to the human being due to high voltage lines can be proved, intense research is undertaken.

In many European countries anyhow maximum limit values concerning magnetic field strengths have been set by authorities which are not allowed to be exceeded by high voltage power lines.

Go back to contents ↑

Reference // Electric Power Transmission and Distribution by Goran Andersson; EEH – Power Systems Laboratory at ETH Zurich