Floating Neutral or Broken (Loose) Neutral
If the Neutral Conductor is opened, broke or lost at either of its source side (distribution transformer, generator) or at load side (distribution panel of a consumer), the distribution system’s neutral conductor will “float” or lose its reference ground Point. Such neutral we call a Floating Neutral.

The floating neutral condition can cause voltages to float to a maximum of its Phase volts RMS relative to ground, subjecting to its unbalancing load Condition. Floating Neutral conditions in the power network have different impact depending on the type of Supply, type of installation and Load balancing in the Distribution.
Broken Neutral or Loose Neutral would damage to the connected load or create hazardous Touch Voltage at equipment body.
In technical article we will discuss the Floating Neutral Condition in T-T distribution System.
- What is Floating Neutral?
- Normal Power and Floating Neutral Conditions:
- Voltage Measurement between Neutral to Ground:
- Various Factors which cause Neutral Floating:
- How to detect Floating Neutral Condition in Panel?
- How to Eliminate Neutral Floating?
- Conclusion
- BONUS (PDF) 🔗 Download Lessons in Electrical circuits, Electrical Machines and Measuring Instruments
1. What is Floating Neutral?
If the Star Point of Unbalanced Load is not joined to the Star Point of its Power Source (Distribution Transformer or Generator) then Phase voltage do not remain same across each phase but its vary according to the Unbalanced of the load.
As the potential of such an isolated Star Point or Neutral Point is always changing and not fixed so it’s called Floating Neutral.
2. Normal Power Condition and Floating Neutral Condition
2.1 Normal Power Condition
On 3-phase systems there is a tendency for the star-point and Phases to want to ‘balance out’ based on the ratio of leakage on each Phase to Earth. The star-point will remain close to 0V depending on the distribution of the load and subsequent leakage (higher load on a phase usually means higher leakage).
Three phase systems may or may not have a neutral wire. A neutral wire allows the three phase system to use a higher voltage while still supporting lower voltage single phase appliances. In high voltage distribution situations it is common not to have a neutral wire as the loads can simply be connected between phases (phase-phase connection).
Figure 1 – Healthy power system scheme
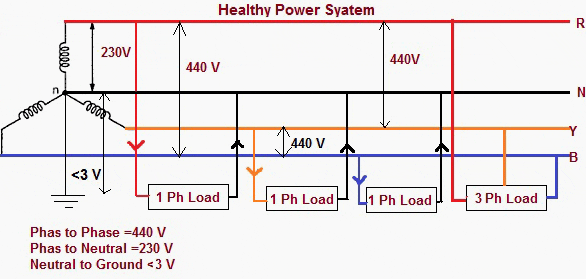
3-Phase 3-Wire System
Three phases has properties that make it very desirable in electric power systems.
Firstly the phase currents tend to cancel one another (summing to zero in the case of a linear balanced load). This makes it possible to eliminate the neutral conductor on some lines. Secondly power transfer into a linear balanced load is constant.
3-Phase 4-Wire System for Mix Load
Most domestic loads are single phase. Generally three phase power either does not enter domestic houses or it is split out at the main distribution board. Kirchhoff’s Current Law states that the signed sum of the currents entering a node is zero. If the neutral point is the node, then, in a balanced system, one phase matches the other two phases, resulting in no current through neutral.
Any imbalance of Load will result in a current flow on neutral, so that the sum of zero is maintained.
For instance, in a balanced system, current entering the neutral node from one Phase side is considered positive, and the current entering (actually leaving) the neutral node from the other side is considered negative.
The same thing happens when we are delta connected, without a neutral, but then the imbalance occurs out in the distribution system, beyond the service transformers, because the distribution system is generally a Star Connected.
The neutral should never be connected to a ground except at the point at the service where the neutral is initially grounded (at distribution transformer). This can set up the ground as a path for current to travel back to the service. Any break in the ground path would then expose a voltage potential.
Grounding the neutral in a 3 phase system helps stabilize phase voltages. A non-grounded neutral is sometimes referred to as a “floating neutral” and has a few limited applications.
2.2 Floating Neutral Condition
Power flows in and out of customers’ premises from the distribution network, entering via the Phase and leaving via the neutral. If there is a break in the neutral return path electricity may then travel by a different path. Power flow entering in one Phase returns through remaining two phases.
Neutral Point is not at ground Level but it Float up to Line Voltage.
If you have flickering lights or tingly taps in your home, you may be at risk of serious injury or even death.
Figure 2 – Floating neutral condition
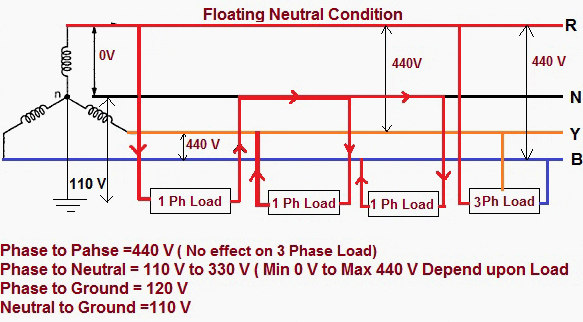
3. Voltage Measurement between Neutral to Ground
A rule-of-thumb used by many in the industry is that Neutral to ground voltage of 2V or less at the receptacle is okay, while a few volts or more indicates overloading; 5V is seen as the upper limit.
3.1 Low Reading
If Neutral to ground voltage is low at the receptacle than system is healthy, If It is high, then you still have to determine if the problem is mainly at the branch circuit level, or mainly at the panel level.
Neutral to ground voltage exists because of the IR drop of the current traveling through the neutral back to the Neutral to ground bond. If the system is correctly wired, there should be no Neutral to Ground bond except at the source transformer (at what the NEC calls the source of the Separately Derived System, or SDS, which is usually a transformer).
Under this situation, the ground conductor should have virtually no current and therefore no IR drop on it. In effect, the ground wire is available as a long test lead back to the Neutral to ground bond.
3.2 High Reading
A high reading could indicate a shared branch neutral, i.e., a neutral shared between more than one branch circuits. This shared neutral simply increases the opportunities for overloading as well as for one circuit to affect another.
3.3 Zero Reading
A certain amount of Neutral to ground voltage is normal in a loaded circuit. If the reading is stable at close to 0V. There is a suspect an illegal Neutral to ground bond in the receptacle (often due to lose strands of the neutral touching some ground point) or at the subpanel.
Any Neutral to ground bonds other than those at the transformer source (and/or main panel) should be removed to prevent return currents flowing through the ground conductors.
4. Various Factors which cause Neutral Floating
There are several factors which are identifying as the cause of neutral floating. The impact of Floating Neutral is depend on the position where Neutral is broken:
4.1 At The Three-Phase Distribution Transformer
Neutral failure at transformer is mostly failure of Neutral bushing. The use of Line Tap on transformer bushing is identified as the main cause of Neutral conductor failure at transformer bushing. The Nut on Line Tap gets loose with time due to vibration and temperature difference resulting in hot connection. The conductor start melting and resulting broke off Neutral.
Poor workmanship of Installation and technical staff also one of the reasons of Neutral Failure.
Under normal condition current flow from Phase to Load to Load to back to the source (Distribution Transformer). When Neutral is broken current from Red Phase will go back to Blue or Yellow phase resulting Line to Line voltage between Loads.
Some customer will experience overvoltage while some will experience under voltage.
4.2 Broken Overhead Neutral conductor in LV Line
The impact of broken overhead neutral conductor at LV overhead distribution will be similar to the broken at transformer. Supply voltage floating up to Line voltage instead of phase voltage. This type of fault condition may damage customer equipment connected to the supply.
4.3 Broken of Service Neutral Conductor
A broken Neutral of service conductor will only result of loss of supply at the customer point. No any damages to customer equipment.
4.4 High Earthing Resistance of Neutral at Distribution Transformer:
Good Earthing Resistance of Earth Pit of Neutral provide low resistance path for neutral current to drain in earth. High Earthing Resistance may provide high resistance Path for grounding of Neutral at Distribution Transformer.
Limit earth resistance sufficiently low to permit adequate fault current for the operation of protective devices in time and to reduce neutral shifting.
4.5 Overloading and Load Unbalancing
Distribution Network Overloading combined with poor load distribution is one of the most reason of Neutral failure. Neutral should be properly designed so that minimum current will be flow in to neutral conductor. Theoretically the current flow in the Neutral is supposed to be zero because of cancellation due to 120 degree phase displacement of phase current.
In Overloaded Unbalancing Network lot of current will flow in Neutral which break Neutral at its weakest point.
4.6 Shared Neutrals
Some buildings are wired so that two or three phases share a single neutral. The original idea was to duplicate on the branch circuit level the four wire (three phases and a neutral) wiring of panel boards. Theoretically, only the unbalanced current will return on the neutral. This allows one neutral to do the work for three phases.
This wiring shortcut quickly became a dead-end with the growth of single-phase non-linear loads.
This Neutral to ground voltage subtracts from the Line to Neutral voltage available to the load. If you’re starting to feel that shared neutrals are one of the worst ideas that ever got translated to copper.
4.7 Poor workmanship and Maintenance
Normally LV network are mostly not given attention by the Maintenance Staff. Loose or inadequate tightening of Neutral conductor will effect on continuity of Neutral which may cause floating of Neutral.
5. How to detect Floating Neutral Condition in Panel?
Let us take one example to understand Neutral Floating Condition.We have a Transformer which Secondary is star connected, Phase to neutral = 240V and Phase to phase = 440V.
5.1 Condition #1: Neutral is not Floating
Whether the Neutral is grounded the voltages remain the same 240V between phase & Neutral and 440V between phases. The Neutral is not Floating.
5.2 Condition #2: Neutral is Floating
All Appliances are connected: If the Neutral wire for a circuit becomes disconnected from the household’s main power supply panel while the Phase wire for the circuit still remains connected to the panel and the circuit has appliances plugged into the socket outlets. In that situation, if you put a voltage Tester with a neon lamp onto the Neutral wire it will glow just as if it was Live, because it is being fed with a very small current coming from the Phase supply via the plugged-in appliance(s) to the Neutral wire.
All Appliances are Disconnected: If you unplug all appliances, lights and whatever else may be connected to the circuit, the Neutral will no longer seem to be Live because there is no longer any path from it to the Phase supply.
- Phase to Phase Voltage: The meter indicates 440V AC. (No any Effect on 3 Phase Load)
- Phase to Neutral Voltage: The meter indicates 110V AC to 330V AC.
- Neutral to Ground Voltage: The meter indicates 110V.
- Phase to Ground Voltage: The meter indicates 120V.
This is because the neutral is “floats” above ground potential (110V + 120V = 230VAC). As a result the output is isolated from system ground and the full output of 230V is referenced between line and neutral with no ground connection.
If suddenly disconnect the Neutral from the transformer Neutral but kept the loading circuits as they are, Then Load side Neutral becomes Floating since the equipment that are connected between Phase to Neutral will become between Phase to Phase ( R to Y,Y to B), and since they are not of the same ratings, the artificial resulting neutral will be floating, such that the voltages present at the different equipments will no longer be 240V but somewhere between 0 (not exactly) and the 440 V (also not exactly).
Meaning that on one line Phase to Phase, some will have less than 240V and some will have higher up to near 415. All depends on the impedance of each connected item.
So, the loads with B-phase will experience more voltage than usual, while the loads in R-phase will experience less voltage. Loads in Y-phase will experience almost same voltage. The neutral disconnect for an unbalanced system is dangerous to the loads. Because of the higher or lower voltages, the equipment is most likely to be damaged.
Here we observe that Neutral Floating condition does not impact on 3-phase load but it impacts only 1-phase load only.
6. How to Eliminate Neutral Floating?
There are some point that needs to be considered to prevent of neutral floating.
6.1 Using 4-Pole Breaker, ELCB, or RCBO in Distribution Panel
A floating neutral can be a serious problem. Suppose we have a breaker panel with 3-Pole Breaker for Three Phase and Bus bar for Neutral for 3 Phase inputs and a neutral (Here we have not used 4-Pole Breaker). The voltage between each Phase is 440 and the voltage between each Phase and the neutral is 230. We have single breakers feeding loads that require 230Volts. These 230Volt loads have one line fed by the breaker and a neutral.
So, be careful with floating neutrals.
Simply use ELCB, RCBO or 4 Pole Circuit Breaker as income in the 3ph supply system since if neutral opens it will trip the complete supply without damaging to the system.
6.2 Using Voltage Stabilizer
Whenever neutral fails in three phase system, the connected loads will get connected between phases owing to floating neutral. Hence depending on load resistance across these phases, the voltage keeps varying between 230V to 400V.
A suitable servo stabilizer with wide input voltage range with high and low cutoff may help in protecting the equipments.
6.3 Good workmanship and Maintenance
Give higher Priority on Maintenance of LV network . Tight or apply adequate Torque for tightening of Neutral conductor in LV system.
7. Conclusion
A Floating Neutral (Disconnected Neutral) fault condition is VERY UNSAFE because If appliance is not working and someone who does not know about the Neutral Floating could easily touch the Neutral wire to find out why appliances does not work when they are plugged into a circuit and get a bad shock. Single phase Appliances are design to work its normal Phase Voltage when they get Line Voltage Appliances may Damage.
Disconnected Neutral fault is a very unsafe condition and should be corrected at the earliest possible by troubleshooting of the exact wires to check and then connect properly.
8. BONUS (PDF): Lessons in Electrical circuits, Electrical Machines and Measuring Instruments
Download: Lessons in Electrical circuits, Electrical Machines and Measuring Instruments (for premium members only):











What a clear and informative discussion of floating ground/neutral. I suspect many folks mistake floating neutral for floating ground. I have run across this condition over the years and now i understand it better than ever, thanks so much, tim10
I am facing one problem. We have installed 1600kVA stabilizer at one of our client location for their Hotel building load. Client had complaint last month that his some fans of chillers & some other equipment which runs on 3Ph voltage has burnt / damaged. when we checked output voltage of stabilizer then we observed that L-N voltage is constant 240VAC in all 3 Phases but there is difference in L-L voltage they are as follows.
1. OUTPUT VOLTAGE: L1-L2 435 V in Fluke Digital multimeter in display its 421V(L1-N 241V)
2. OUTPUT VOLTAGE: L2-L3 411 V in Fluke Digital multimeter(L2-N 242V)
3. OUTPUT VOLTAGE: L1-L2 408 V in Fluke Digital multimeter.(L3-N 241V)
My question is will this be case of floating neutral? because L-N voltage is stable but L-L voltage is getting changed bit confusing.
I have a picture, do you have an email address I can submit a picture to..it’s regarding a floating ground on a transformer that is configured x1 h3 x2 xo h1 x3 h2 solar field 480 to 208
We have developed a voltage protector that can be installed in main line to protect against 440V. We have design it so that it can withstand 440V for indefinite period of time.
Let us know if we can be of help in any such cases.
9769996205
“ Power flows in and out of customers’ premises from the distribution network, entering via the Phase and leaving via the neutral.”
The above is not correct, Sir. Power (actually, energy) doesn’t flow from source to load through the phase wires and from load to source through the neutral wire.
It can be proven that in a purely resistive load, energy flow is unidirectional, at all instants of time it flows from the source to the load, through both the phase and neutral wires.
It can be proven that in a purely reactive load, energy flow is bidirectional, for half a cycle (of the instantaneous power, which corresponds to a quarter cycle of the instantaneous current and voltage) it flows from the source to the load, through both the phase and neutral wires; for the other half cycle, it flows from the load to the source, through both the phase and neutral wires; the average energy flow (average power a.k.a. active/real power) is zero.
It can be proven that in a resistive-reactive load, energy flow is bidirectional, for some fraction of one cycle (of the instantaneous power) it flows from the source to the load, through both the phase and neutral wires; for the remaining fraction of the same cycle, it flows from the load to the source, through both the phase and neutral wires; in this case, more energy flows from source to load than from load to source, meaning there is a (non-zero) average energy flow, meaning the load consumes an average or active power.
Read about the Poynting vector.
“ If the Star Point of Unbalanced Load is not joined to the Star Point of its Power Source (Distribution Transformer or Generator) then Phase voltage do not remain same across each phase but its vary according to the Unbalanced of the load.”
The above statement is wrong or misleading. It says that in unbalanced conditions, phase voltages aren’t the same if we have a floating neutral. While that is true, the phase voltages will still be unbalanced even if we have a grounded neutral.
while using two source one city line and another generator line for redundancy then connected to ups then iso transformer(delta star) can this iso transformer be by passed using a DB while using the neutral from the same iso transformer for already connected load ..using 3pole mccb for the bypass DB
We had a peculiar problem.
The Voltages on main LT panel (Out going of transformer), the Voltages are balance d 600 ph to ph.But R to G is 600V,B to G is 13V and C to G is 575V.
Current readings on the starter are balanced.
Can anyone know the reason and how to address this
The break in the neutral wire from the distribution transformer to the domestic supply has caused extensive damage to so called ‘smart’ appliances such as refrigerator with an electronic mother board, desk top computer, inverter, phone chargers and voltage stabilisers for all these appliances. A 4 pole mcb at the main switchboard might prevent such an event.
So good.
What is the effect on energy consumption of a three phase high load consumer due to floating neutral
At my single family house in Florida I have just had a problem with a bad Neutral from Electric supplier (FPL) into my home…
the way I noticed the problem was I received a shock from metal shower handle when taking shower, lights flicker and AC Handler damaged blower motor
Now very concerned with the life safety of my house for my family and myself
Any other steps you can offer for me to have done as far as more grounds installed or something my electrician or FPL could do that would protect the home if that would happen again form FPL
thanks for any advise you can provide
Pat
FPL did come out said it was there bad neutral line and made repair to splice connector at transformer and supply line
Excellent Essay…
This What We Call Comprehensive Informative Job
PowerElectronics Engineer
Wael Mostapha Hael
Yemen-Adan
Can it be advisable to connect neutral point earthed of a 3-phase 3 limb core Potential Transformer in Switchgear Panel ? As Switchgear Panel is of metal sheet & Source Earthed is connected to the metalic body through conductor. If external current flow through neutral the flux of PT may increased & in turn Vol;tage also will be increased which may result failure of Insulation of pt & it may damaged . Please give your valuable opinion . Also suggest for connection of Multi-function 3-PHASE , 3-WIRE meter across PT
Neutral was floating at power pole and we were getting 308volts. I switched off all buttons, even with buttons off will there be problem to appliances due to floating neutral?
is neutral earthing in servo stabilizer will solve the problem of Neutral Floating. if we use the stabilizer between the mains and the load
Very nice explained and useful article
If we load to gen the neutral shocks but on nepa it is normal why?
Could you please clarify during occurence of a neutral alive fault, why only some consumers’ equipment are damaged with overvoltage while other consumers on the same phase do not suffer from equipment damage? (T-T system used in my country.)
I guess author made this point already “Some customer will experience Overvoltage while some will experience Low voltage”. This happens due to neutral line will be close to one of the lines. I think the lines in-phase will have overvoltage and out of phase will have low voltage.
Thank You for your explanation.
Request you to kindly clarify what would be the immediate effect of neutral break on LV switchgear 4Pole MCCB, ACB or MCB will they get trip ?
Regards,
Very nicely explained .Thank you very much
Halo,
Thanks for explanation, it answered problem in our gantry crane last week. There was a losing neutral terminal on secondary side of 3 phase step-down transformer, 500/400, then voltage should be 230 V L-N became 380 V L-N. Measured on Line- Line (V1-V2, V2-V3, and V3-V1) voltage found 400 V. so, strange. 4 PSU found burned.
Then, we tightened losing neutral terminal. Hola!. problem solve but did not know the explaining until I read your article. thank, bro.
Nicely explained,
Hi, we have control transformer of primary 430 v, secondary 110 v ac.
Secondary side 0 to earth is showing 32 v, how to rectify this. Normally 110v neutral to earth is showing 32 v.
Please help me
The article is informative, let me ask when the Distribution Transformer Neutral bushing damage/failure means how the phase voltages are frequently fluctuating higher level? is this due to phase load varies ? or producing from Transformer itself?
I cant understand how a 4 pole breaker will trip the incoming supply. I wonder if a ELCB, RCBO, will either help to trip the incoming supply in case of a floating neutral.
Neutral to ground voltage of UPS is 14 vac at UPS outgoing panel and UPS DB on day time with load but after load reduce neutral and ground voltage also reduce what is the reason behind can any one suggest.
Nice one
Hello Sir,
I have seen many LT panels having earth bus bar insulated. Why earth bus needs insulation??
hi sir
i had an experience, one day all the equipment in my home where showing earth and much enough power to through us out ,we all are scared ,i checked every where and finally found that incoming line of meter (service connection from utility) got short and was stick in the meter box, i rectify that, but the most worst thing is we got 10000 RS BILLED FOR THAT DAY FROM KSEB, MY DOUBT IS THE INCOMING LINE(BEFORE METER) GOT SHORT, THEN HOW THE METER WILL READ IT?
Under neutral floating condition why neutral to ground voltage is 110 and phase to ground voltage is 120v
Sir
My question is that when Earth fault or over current fault occur in a 11 KV feeder, some high voltage occur in substation LT AC and same in DC and sub Station SCADA Relay and equpiment burn many times and this type of problem occured in many sub stations. what is the cause of this and what is the solution.
Thanks
Is there any reason why the phase-voltage (between line-to-neutral) i.e. RN, YN, BN is shown 230V but the line-voltage (between line-to-line) i.e. RY, YB, BR is shown 440V. With phase-voltage 230V, the line-voltage should be 400V, not 440V. This excellent article is being tarnished by this omission.
Dear Mr. Parmar
Thanks for the useful information. Yet, I still don’t get the idea why neutral-grounded cable could not be a source of one fault current since it is connected to ground? I would really appreciate your answer
Any Neutral to ground bonds other than those at the transformer source (and/or main panel) should be removed to prevent return currents flowing through the ground conductors.
In the above statement, i need more clarity and please explain about multiple neutral earthing.
Do we need to earth the Neutral point at our incoming supply in house wiring. (ie. Before meter).
If we earth , does it cause any harm, how?
or else neutral earthing at transformer itself is sufficient.
Today i understood that what is neutral floating….
very very Thank u sir for giving this information….
We have a system with 132kV/110V Instrument Voltage Transformer. Primary is A-N, B-N, C-N with N is earthed. Secondary is 3 phase – 4 wire system i.e. a-n, b-n, c-n with n earthed. On secondary there is an Inter-posing VT-IVT (3 phase single unit) with Y-y connection and primary is connected to main VT a-n, b-n, c-n through fuse / link. Neutral of secondary of IVT is also earthed. This circuit is for synchronization via voltage selection scheme.
During injection on secondary of main VT and checking fuse failure condition (by removing one wire from the injection kit & giving 2 phase voltage to VT secondary circuit) all three phase voltage found on the primary of IVT and in-turn secondary.
Please guide to avoid the reflected voltage in third phase of IVT for which the wire was removed.
The neutral should never be connected to a ground except at the point at the service where the neutral is initially grounded (At Distribution Transformer).
Dear Mr.parmar
We have the same problem in our distribution LV network (I mean stolen of neutral wire). My question is how the floating neutral condition can be detected? Pls. answer this question from distribution company engineer standpoint.
The second figure (entitled “Floating neutral condition”) clearly describes this situation and it can be revealed that voltage measurement and voltage deviation is a good method to detect neutral opening condition.
But if broken neutral occur in middle of distribution line, transformer side neutral voltage will not deviate extremely (because of loads that are exist between transformer and opened point) and voltage measurement based method will not be good remedy.
Then, please share with us your valuable opinion.
BR
In radial distribution system, measure the end of road voltages using the same method. Or randomly measure voltages at consumer’s Energy Meter input terminals will solve your issue I think.
hi! in ups mono phase 220-240v input , output 220v when i test N to ground has 110v why?
Hi..
in AC Single phase circuit why not switching neutral wire..? only using single pole breaker to switching hot wire.
Neutral must not be broken, when chance for the equipment is still live.
if single phase voltage is 230v and three phase voltage 400v then what is two phase voltage it so?
I think I know the answer but lets see… In an environment where 220 = (2) 110 180 degree out phase…..and netural from line transformer is also supposed to be earthgrounded….. basic residential….. with no load environment between 220 nor 110 to netural…. Then idealy meter readings from incoming netural to earthground should ideally be.. 0, volts… 0,current, impediance/resistance less than 10k oms…..
And if at panel incoming source from line transformer has no load and earthground is disconnected from netural…. And meter is placed between netural and earthground…. And reads .5 + amps…. 11-33 volts…. Then one could assume that a floating netural condition exists…. And if netutal is center taped from line transformer and earthgroumded… Then would it be safe to assume that line input to transformer. Is in- correctly phased at its point of orgin and have a possible floating netural … Causing subquent line voltage to attempt to balance with and in proportion to load variances on said line…. Which depending on source of line voltage could result in phase variance occuring…. In line voltage along with frequency instabilities…… And if so as such occurring… Wouldn’t these conditions end results be….
At panel…
Basically no detectable error in 220 (accross) (2) 110’s @ 180 degree out of phase… And no detectable error in either of 110 to netural… Except during peak loading times aka work days occasional voltage difference of 5-7 volts only in of 110’s…. but as such would produce no noticiable variances to consumer….. It would result in usage meter being affected producing heavly exaggerated usage amounts falsely due to noticable current and voltage levels existing between earthground at panel incoming netural with said being disconnected from one another……… Seriously I’m just trying to determine what is source of exagerated usage meter readings… I know myself that i have over past 36 months reduced number of occupants from 4 to 1…. And with even implementation of mains shut off when not physically present… Hot water and well water pump being kept of unless usage is needed…. And no god awful rate increases….. My metered usage is being reported to have increased almost 200 percent…. And its not isolated… All consumers on service provider have same claims and obversatioms…. I don’t have access to my osssocilope at this time or i would be investigating with a more visual presence
….. Thank you for taking time to read my question…
Donny, Wrong assumption, a split phase system does not get its power from a two phases 180 degrees apart (this is a common erroneous belief), that would give 0 volts. It splits the transformer via a center tap, so line to neutral only utilized half the transformer, line to line uses the whole. Ungrounded, a current flow reading neutral to ground is normal, as this is not a 3 phase system (actually single phase) the total voltage across the lines (not phases) never goes to zero. Current divides according to resistance, so in the parallel path created by ground and neutral current would mostly flow via the nuetral, but not all.
useful details and good approach
Article is very interesting for the elect power dist network engineers who are always working in the site. In my country and the others poor countries the robbers always cut and stole the grounding copper conductors which earthing the transformers and distribution panels and make the earthing circuits are open the customers equipments becomes in mal operation and the elect workers life in the network will be unsafe
Hi, Alpha transformers has designed powerguard which do not allow double phase 440v to pass to the household electronic device when there is neutral breakdown. Pls visit our website http://www.alphatransformers.in for more info
Hi
Please help/explain. We had a theft of a neutral bus bar at the sub station (common in my country). This resulted in some people’s houshold appliances malfunctioning. I’ve read your explanation about the conditions which develop as a result of no neutral.
Can you please explain what happens to household appliances when this condition occurs. Does the condensor get damaged. Please help.
Very good explanation, though it is simple still quite informative.
En Lima, capital del Perú el sistema de baja tensión es 3 x 220 V , 60 Hz. es decir que no hay neutro. Tampoco hay linea de tierra .Todas las cargas se colocan entre fases y nadie se atreve a tocar un cable pues recibe un susto muy grande. No existe el problema de subir de 220 a 400 V y dañar los equipos instalados.
Very useful article
hello mr.parmar. thank you for your explanation. I have the same problem several month ago. lamps light on my home become flicker suddenly. firstly i think just common problem, but it was happened everyday, until died one day. I still think that it just source generation problem, but after 3 hour, i felt there is something wrong, why still die??, i am decided to check the fuse, i replaced it with the new one, but nothing changed. then i ask to my friend to checked it. and we opened the KWH meter panel, and he said that the neutral was broken. even i am electrical engineer, i always afraid with electric shock. and then my friend help me to conjunct the neutral. And then electrical back to normal condition. i have some question:
1. How to eliminated the neutral floating on 1 phase load (home), whether we have to use power stabilizer?, if yes, how to install it? is on each of equipment or not?
2. How large voltage and current that can make bad shock in human body, in which can make die?, exactly i am always afraid, bad afraid in electrical,,some times i feel so stupid because i am electrical engineer.
thank you