Programming of microprocessor relays
Developing basic setting specifications for numerical relays is a boring process for most electrical engineers, but not for the protection engineers! It requires significant input data but, for the most part, is exciting and relatively straightforward.

A basic understanding of Boolean expressions and methodologies is helpful in developing the required programing to obtain the desired logic and for effectively using the full power that is designed into numerical relays.
The capabilities and power that are built into microprocessor relay designs are continually expanding. In addition to providing an array of protective functions, capability to fulfill most of the control and data acquisition requirements at substations is provided.
Many modern numerical relays possess the power to replace other digital devices that are required within substation control and data acquisition systems such as PLCs, RTUs, meters, and control switches.
Protection engineers are not necessarily proficient in programing techniques and, as such, they may be hesitant to apply numerical relays such that their full capability is used.
Programming tools
An understanding of programing techniques is required to effectively use the many features and flexibility that are designed into modern microprocessor-based relays.
Programing tools available for programing modern numerical relays include:
- Boolean Algebra
- Control Equation Elements
- Binary Elements
- Analog Quantities
- Math operators
- Relay settings
Also, let’s mention the enhancements achieved by numerical relays in distribution and transmission system with mentioning of some most typical examples:
1. Boolean Algebra
Knowledge of Boolean algebra and its relationship to logic created by electrical circuits is important to facilitate the task of programing numerical relays.
Many good texts and courses are available for obtaining knowledge of this subject area. A brief overview of some basic fundamentals follows.
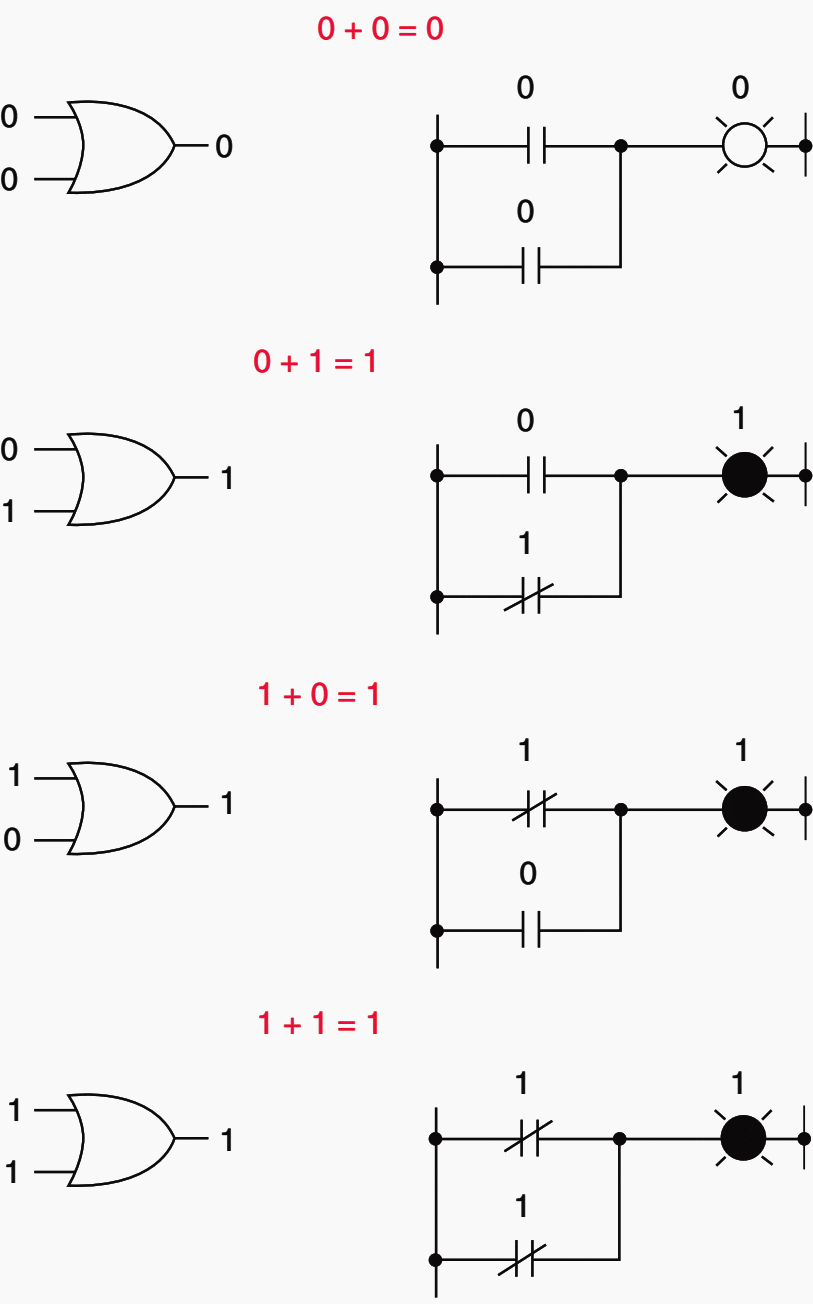

In Boolean arithmetic, terms can only have two states—they can be either a 1 or a 0. Rules for Boolean addition are illustrated in the following equations:
0 + 0 = 0, 0 + 1 = 1,
1 + 0 = 1, 1 + 1 = 1
It does not matter how many terms are added, the sum cannot be any larger than 1 since, as noted earlier, only 1 and 0 can exist:
0 + 1 + 1 = 1,
1 + 1 + 1 + 0 = 1,
1 + 1 + 0 + 1 + 1 + 0 = 1
Boolean addition corresponds to the logical function of an ‘‘OR’’ gate and is representative of parallel contacts in an electric circuit. The basic equations for Boolean addition along with its logical ‘‘OR’’ gate and electric circuit representation are illustrated in Figure 1 above.
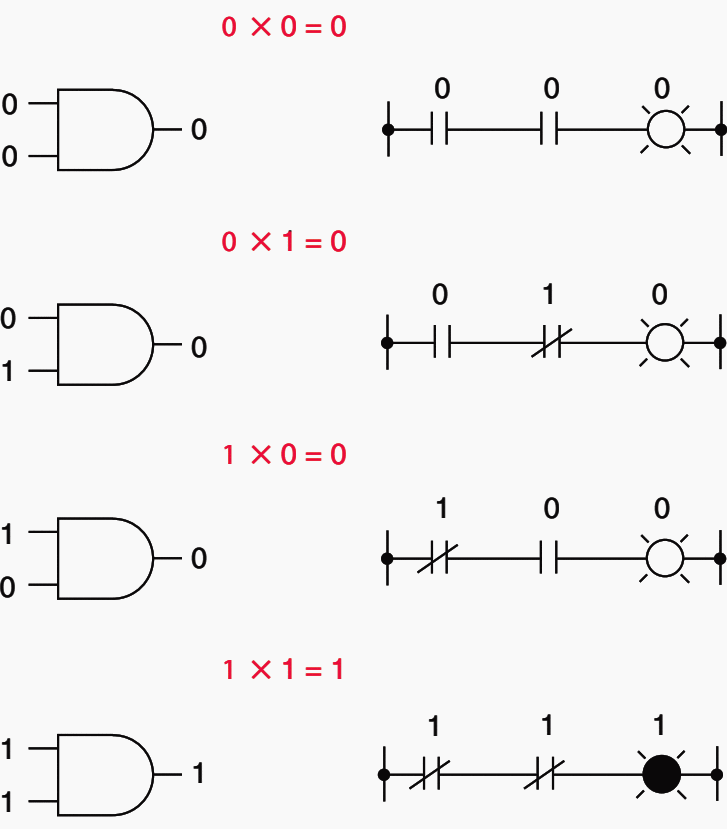
Following are the equations that represent the rules for Boolean multiplication:
0 × 0 = 0,
0 × 1 = 0,
1 × 0 = 0,
1 × 1 = 1
Boolean multiplication corresponds to the logical function of an ‘‘AND’’ gate and is representative of series contacts in an electric circuit.
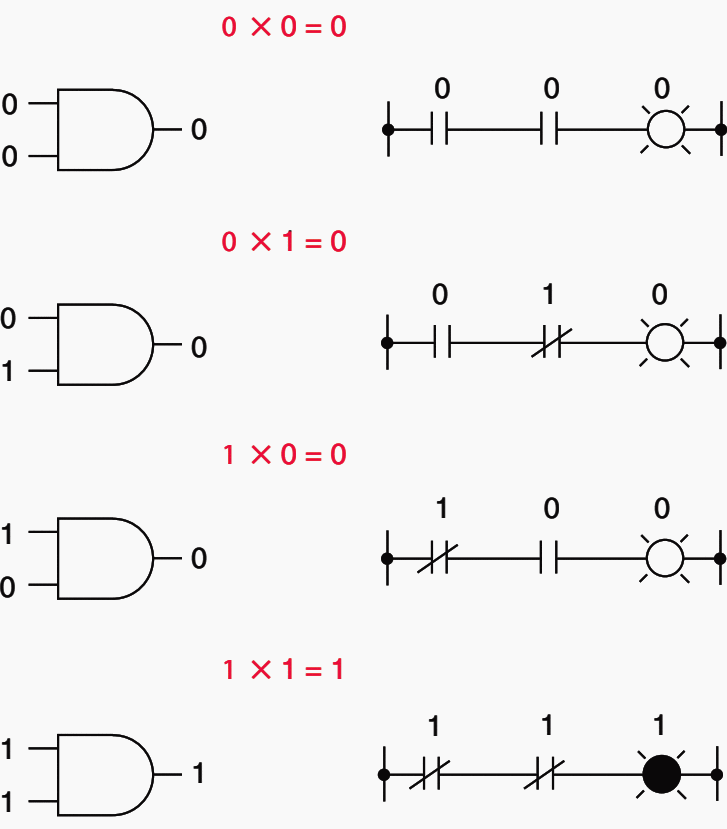

Figure 2 illustrates expressions for Boolean multiplication. Boolean algebraic variables are denoted by capital letters.
A complement is referred to as a logical inversion and corresponds to the logical function of a ‘‘NOT’’ gate.

Electrically, a logical inversion is equivalent to a normally closed contact. Expressions for Boolean complementation are illustrated in Figure 3.
As in mathematics, identities also exist in Boolean algebra. These identities are derived from the unique bi-variable nature of Boolean variables.
Basic Boolean additive and multiplicative identities are illustrated in Figure 4 below.


Boolean algebra also contains cumulative and associative properties.
- Cumulative property of addition: A + B = B + A
- Cumulative property of multiplication: AB = BA
- Associative property of addition: A + (B + C) = (A + B) + C
- Associative property of multiplication: A(BC) = (AB)C
- Distributive property: A(B + C) = AB + AC
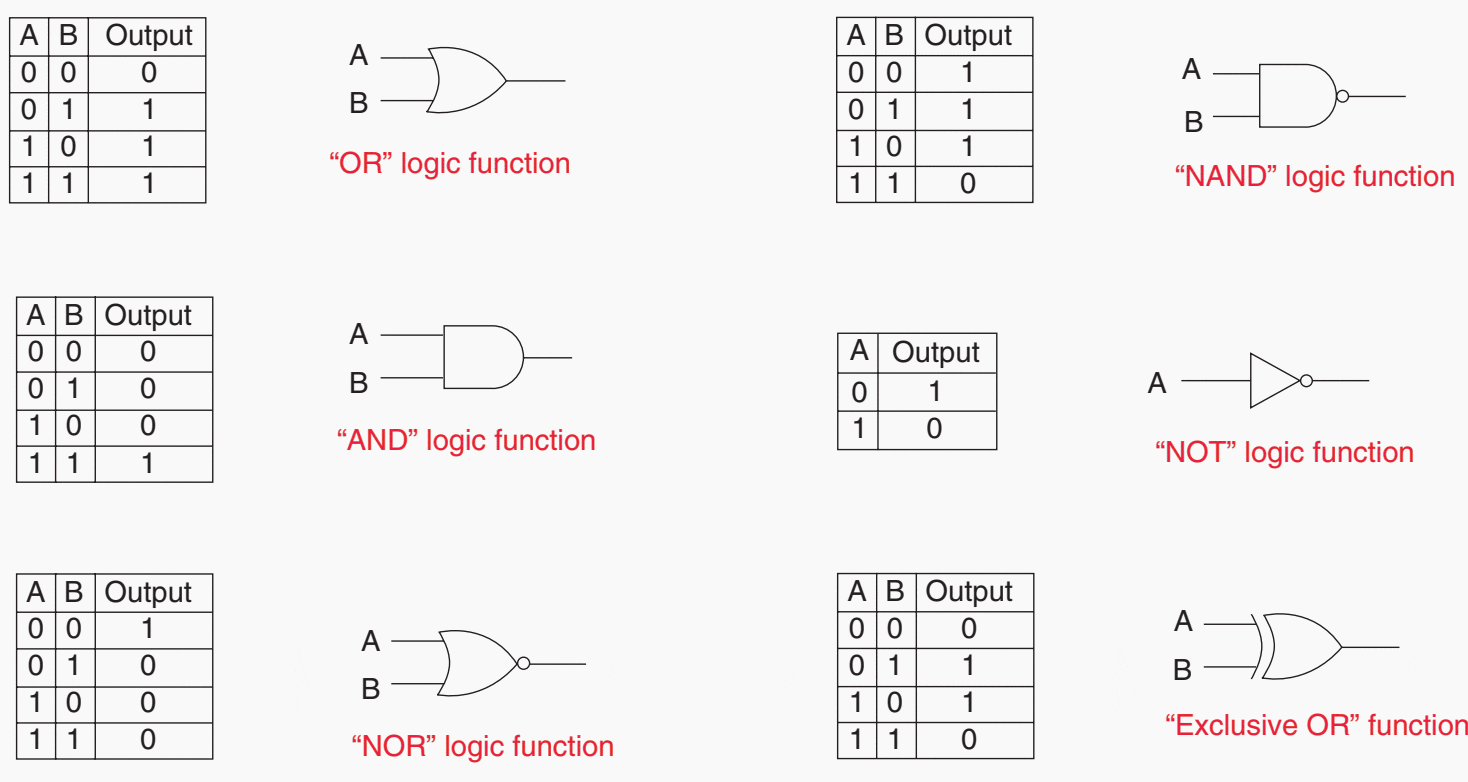
Some other operators used in Boolean expressions include comparisons (<, >, = , etc.), parentheses, and rising and falling edge triggers. Numerical relays often use symbols to represent Boolean operators (i.e., + = OR,* = AND, ! = NOT).
To promote programing efficiency, the initial expressions developed from the truth table should be reduced, using the laws of Boolean algebra, to a simplified form. The required logic circuit can then be developed from the simplified expression.
Figure 5 illustrates truth tables for a variety of logic gates used in logic diagrams.

Example
The following example illustrates the process of developing logic for control circuits:
Three pilot relaying systems are applied on a very important transmission line. In order to enhance security of the line it is desired that trip outputs from two out of the three pilot systems must be present for a trip of the line to be initiated.
A1 represents a trip output from a pilot scheme and a (0) represents no trip output from a pilot scheme. The associated truth table would look as
shown in Table 1.
A’ will be used to indicate a complement. From the four conditions in the truth table for which an output is indicated, the following Boolean equations can be developed:
Table 1 – Truth Table for ‘Two–Out–Of–Three’ Pilot Logic
| Pilot 1 = A | Pilot 2 = B | Pilot 3 = C | Output |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Line 4 – A’BC = 1
Line 6 – AB’C = 1
Line 7 – ABC’ = 1
Line 8 – ABC = 1
A Boolean equation could then be developed to cover the conditions given earlier:
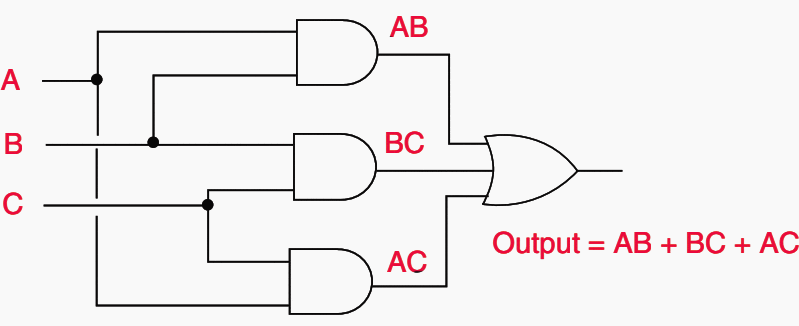
Output = A’BC + AB’C + ABC’ + ABC
A logic circuit could be developed to match the Boolean equation stated earlier. However, it would be rather complex. By using rules of Boolean
algebra, the aforementioned equation could be reduced to:
Output = AB + BC + AC
Whereas the logic requirements for this case were more or less intuitively obvious as the required logic was quite simple, for more complex systems it is easy to develop errors when shortcuts are taken and intuition is used instead of a step-by-step process.
The associated logic circuit for the aforementioned output equation is illustrated in Figure 6 below.

2. Control Equation Elements
Control equation elements are a collection of storage locations, timers, and counters that are available in the relay for the user to customize the operation of the relay and to provide logic in data for substation automation.
They also provide storage locations for remote bits that are communicated to the relay to identify the status of other equipment.
3. Binary Elements
Binary elements are the outputs that are the result of internal relay logic. The logic that controls the binary elements can be pre-programed or programed by the user.
Binary elements can be used in Boolean equations to create other logic or to initiate various actions such as the trip output, close output, triggering of an event report, and so on.

4. Analog Quantities
Analog quantities are current and voltage quantities that are received, measured, and calculated. Analog quantities may be instantaneous, average, or RMS values of the associated current or voltage.
Math operators are used to program the analog quantities.
5. Math operators
Math operators are used for writing mathematical control equations using analog values. Math operators include familiar operations such as addition, subtraction, multiplication, division, square root, logarithms, exponents, trig functions, and so on.
Programing mathematical equations by the user is usually associated with control functions rather than protective functions.
6. Relay Settings
In addition to programing for logic equations, microprocessor relays require inputs to assign the level and time delay at which various binary elements change state (set points for protective functions, timer setting, etc.) and to enable or disable various functions that are available in the relay.
Many numerical relays provide for a wide selection of protective functions that can be selected for use along with a number of setting groups in which different settings can be applied.
Only one setting group can be active at one particular time. The different settings in the groups can be applied to provide the required protection for different operating conditions.
In dealing with such large amounts of data, the protection engineer must compile the input requirements with care and due diligence to avoid errors. A simple slip of a digit or an incorrect sign can have serious negative impacts on the reliability and safety of the related power system.
Protection Enhancements
Significant features of microprocessor-based relays that serve to enhance protection previously available through application of traditional relaying include the following:
- Numerical relays allow for a variety of protection systems to be applied with minimal additional cost.
- Changes can be made within microprocessor-based relaying systems with ease.
Application of microprocessor relaying systems along with a local area network provides a means to easily modify logic and settings and to easily apply protective schemes that previously could not be justified.
Distribution Protection Systems
The use of microprocessor-based relaying at distribution substations has allowed for the application of protective schemes that previously were too complex or costly to be justified.
Breaker failure relaying has been sparingly applied in the past at the distribution level because of the complexity and cost involved with electromechanical breaker failure schemes.


With microprocessor-based relaying, it is also a relatively simple matter to provide backup relaying for protection applied on distribution lines.
Backup protection can be obtained by programing the alarm contact of each feeder relay to trip the associated feeder breaker with permission from the operation of a backup overcurrent relay. Closing of the alarm contact occurs when the self-checking mechanism of a relay indicates a problem within the relay.
Overcurrent relaying that is supplied by current flowing through the substation transformer, in many cases, is applied for bus or transformer protection. The overcurrent elements that exist for this relaying can be used for the overcurrent supervision function for the feeder backup protection at minimal additional cost.
For faults on a feeder, if sufficient fault current exists to pick up the bus overcurrent relay, the blocking overcurrent relay on the faulted feeder will also always operate and block tripping of the bus protection. If the fault is on the bus, none of the feeder overcurrent relays will operate, and the bus scheme will operate after a short time delay.
A time delay of about six cycles will usually be sufficient on the bus scheme.
Larger three-phase motors may be individually protected against unbalances. Smaller three-phase motors and single-phase motors, however, may not be equipped with such protection.
Utilities have received many complaints and lawsuits on account of the motors that have failed when continued operation of a distribution substation with a blown high-side fuse was allowed.
Refrigerator and air-conditioning motors are especially vulnerable under such conditions and one substation may supply many hundreds of such motors.
Application of microprocessor-based relays makes it relatively easy to detect the earlier mentioned blown fuse condition at distribution substations. Microprocessor relays are usually equipped with undervoltage elements that can be programed to detect voltage conditions representative of a blown high-side fuse on a delta–wye connected transformer and to initiate appropriate action to disconnect affected loads.
Typical settings that could be programed into the relay might be such that an output is initiated if, at the same time, any phase-to-phase voltage is less than 40% of nominal AND any phase-to-phase voltage is above 70% of nominal.
Such a setting will detect conditions that exist for a blown high-side fuse condition but will not initiate an output for a blown fuse on the potential transformer that supplies the relay. For a blown PT fuse, two lowside phase-to-phase voltages drop to 58% whereas the other phase-to-phase voltage remains normal.
The ability to automatically change settings on numerical relays can also provide beneficial flexibility at distribution substations. Settings can be reduced at light load conditions to obtain greater sensitivity for fault coverage.
Transmission protection Systems
The flexibility provided by numerical relays can provide significant benefits for protecting transmission systems. Many of the microprocessor-based relays that are designed for transmission line protection offer a variety of distance characteristics that can be selected by the user.
The best characteristic that fits a particular application can therefore be applied and easily modified if system conditions change.
For example, for a short line, a quadrilateral characteristic might be best to provide the desired arc resistance coverage. For long lines, distance characteristics that are specially designed to provide immunity from operating on load are available on many numerical relays.
If the system is rearranged such that short lines are made longer, long lines made shorter, or multiterminal lines are created, the related distance characteristics can easily be changed to best fit the specific need.

Higher voltage substations often use a bus tie breaker that can be substituted for any line breaker. The bus tie breaker is ideally used when a breaker is taken out of service for maintenance or on account of a failure of the breaker.
With multiple setting groups that are available on most numerical relays, application of such relays on bus tie breakers allows the settings to be easily changed to match those requirements for the particular line for which the tie breaker currently provides termination.
Transformer differential protection using SEL487E
To implement the differential protection setting on the power transformer in the Digsilent Power Factory environment using SEL487E relay model.
Sources:
- Protective Relaying Principles and Applications by H. Lee Willis and Muhammad H. Rashid
- SIPROTEC protection relay 7SJ62/64 manual











im happy to be a member
Dear Respected Engineer,
Kindly accept my Morning Wishes and Greetings.You deserve for it since you help others by sharing ur Knowledge and Wisdom,thanks for all.
I want to grade on Instantaneous settings between feeders ,LVs and group control breaker in a sub station.Feeder CT’s have Feeders 4 Nos -400A/11KV,LV’s 1200A/11KV and GC 600A/110KV having all 1A secondary ,TRANSFORMER 16 MVA @110 KV/11 KV with Z 10.05%.
we need Instantaneous settings with Gradings,If possible Kindly Help
With Best regards
KATHIRASAN,
PROTECTION ENGINEER,
RE POWER AREA ,INDIA
+91-9962214600
[email protected]
I will love to have a sound knowledge of control systems, specifically programmable control systems.
Dear Sir,
it seems that Fig.3 is not correct.Please check it.
Best regards
M.A.Khorshidi