The loss of phase
The most common cause of unbalance for three-phase motors is the loss of phase resulting from an open fuse, circuit breaker, connector, or damaged conductor. Unbalances in other connected loads can also affect the motor. A voltage unbalance of 3.5% can produce a 25% or greater increase in motor temperature. This results primarily from negative sequence produced by the unbalance.

This current produces flux in the motor air gap rotating in the opposite direction to the actual motor direction. The relative effect is essentially double-frequency current in the rotor. Skin effect results in higher resistance, and negative-sequence impedance remains essentially at locked-rotor value. Thus, high current and high resistance compound the heating effect.
The total heating in a motor is proportional to: I12 + K22×t (equation 1), where,
- I1 and I2 are the positive- and negative-sequence currents, respectively, in the motor
- K = Rr2 / Rr1 = conservative estimate as 175 / ILR2 (equation 2)
where,
- Rr1 and Rr2 are the motor rotor positive- and negative-sequence resistances, respectively,
- ILR the locked-rotor current in per unit.
For any specific case, this circuit can be expanded to show more detail of the source or other loads. The supply transformer, for example, can be represented by its reactance (impedance) XT.
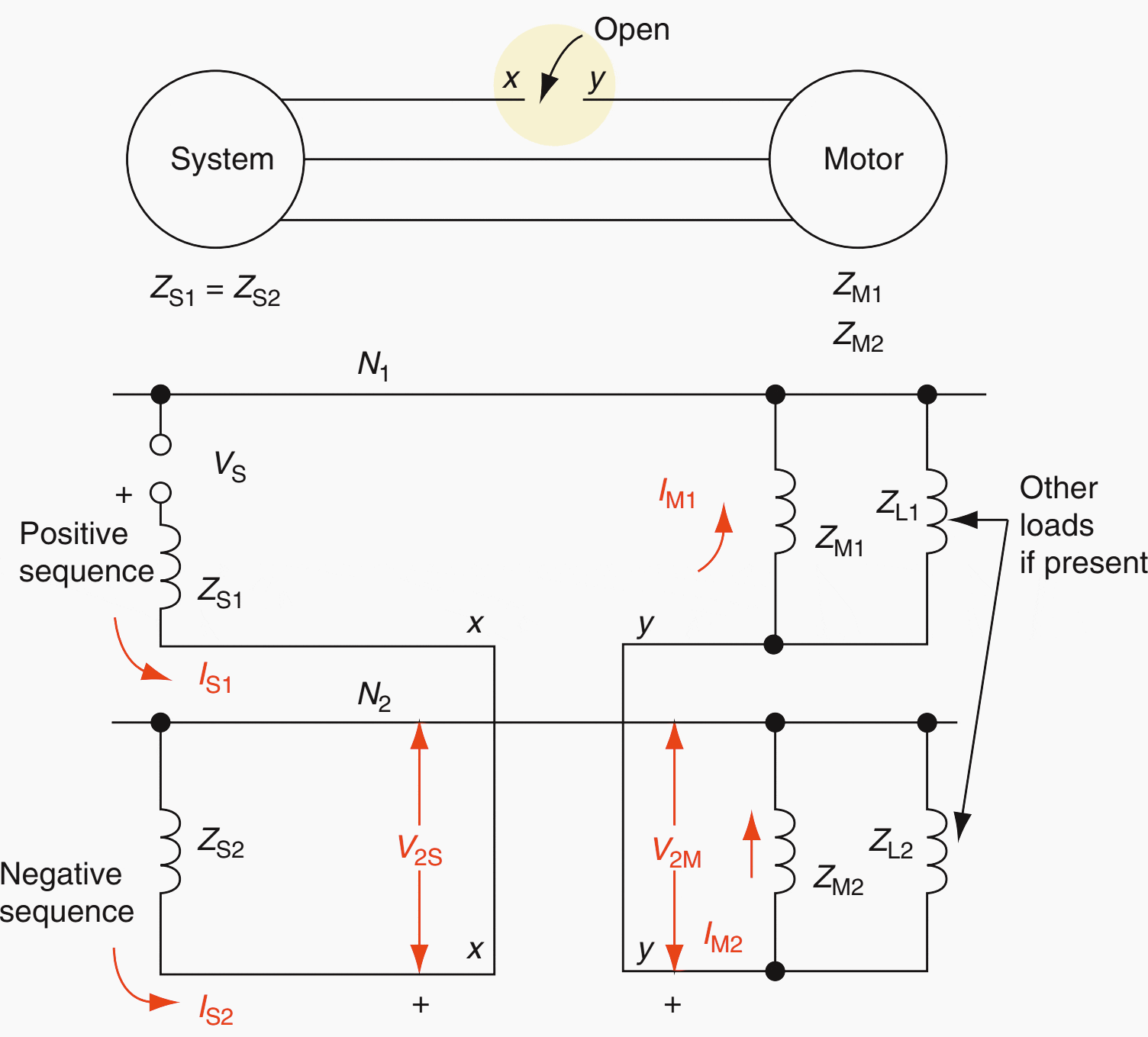

For an open phase between the transformer and motor, XT would be added in series with the source impedances for the equivalent values of ZS1 and ZS2. When the open phase is between the system and the transformer, XT would not be included in the source equivalents, but added in series with the motor impedance.
This circuit is for an ungrounded motor, as is the common practice.
The distribution of currents for an open phase using the network of Figure 1 is shown in Figure 2 for several situations.


Typical per unit values of impedances shown are all on the motor kVA base, and are:
- ZS1×ZS2 = 0.05 ∠90° pu,
- ZL1 = ZL2 = 1.0 ∠15° pu for static loads at the motor,
- ZM1 = 0.9 ∠25°,
- ZM2 = 0.15 ∠85°.
These angles were included in the calculations, but the simplification of assuming all impedances at the same angle gives close approximations and does not change the trends shown. With all values at 90°, for example, IS1 = 0.87 pu instead of the 0.96 pu in Figure 2.
From these sequence currents, it is observed that on either side of the open Ia = I1 + (−I2) = 0 correctly. The sound phase currents are (when I1 = −I2):
- Ib = a2I1 + aI2 = −j√3I1
- Ic = aI1 + a2I2 = +j√3I1
so in Figure 2, Ib and Ic currents are 1.66 pu. Thus, it is seen that an open phase provides very low-phase currents relative to the normal motor-load current of about 1 pu. Consequently overcurrent relays are not adequate to detect an open phase.
The power is transferred across the motor air gap and reduces the motor shaft power so that pullout may occur.


One example that is indicated shows that the motor would pull out at 20% of rated load, with static load three times larger than the motor load; or at 50% of rated load, with static load equal to the motor load. In addition, the low value of the motor negative-sequence impedance implies that a large portion of negative-sequence current flows in the motor to increase heating.
This distribution is illustrated in Figure 3 above.
The motor negative-sequence current can be low, as shown in Figure 4 below, only when the static load is single phased.


The fundamental for an open phase is that the positive- and negative-sequence currents are equal and opposite as long as zero sequence is not involved. This is useful to develop the unbalance currents through wye–delta transformer banks.
These, as well as the calculations in Figure 2, 3 and 4 are for the conditions immediately after the phase opens and before the motor slows down, stalls, or its internal impedances change, and so on.
The current directions shown in the circuit diagram for these two figures are correct for the phasor diagrams. Without these specific phasor diagrams, the IB in Figure 5 could be shown into the motor as indicated, but at √3 magnitude with IC at √3 flowing to the source. This is actually the flow, and is indicated in Figure 5 by the phasor diagram, showing that IB flows as indicated, but IC is 180° from IB, both at √3 magnitude.
If IB and IC were shown in opposite directions in the circuit diagram, the correct phasor diagram would be to show IB and IC in phase. These currents can be traced through the transformer with the unbalances indicated, recalling that 1.0 pu current in the wye winding appears as 0.577 pu current in the delta winding.
Negative-sequence voltage can be used to detect unbalance in motor circuits. By fundamental definition V2 = −I2Z2. With reference to the example of Figures 2, 3 and 4, the per-unit negative-sequence voltages on the two sides of the open phase for situations a and b would follow.
For situation c, V2S = V2M because there is no open phase between the supply and the motor.
| CASE A | CASE B | |
| V2S = | 00.96 × 0.05 = 0.048 | 1.6 × 0.05 = 0.080 |
| V2M = | 00.96 × 0.15 = 0.144 | 1.5 × 0.15 = 0.227 |


When the open phase is downstream or between the V2 measurement and the motor, the negative-sequence voltage relay will ‘‘see’’ V2S, which can be quite low because of the low-impedance source. When the open phase is upstream or between the V2 measurement and the supply, the relay will ‘‘see’’ V2M, which is generally larger.
Thus, negative-sequence voltage is most useful for upstream open phases, with phase-current comparison for the downstream ones.
Unbalance and phase rotation protection
As suggested in above paragraphs, there are several handles available for unbalance detection:
- Magnitude differences between the three-phase currents,
- The presence of negative-sequence current, and
- The presence of negative-sequence voltage. All three are used for protection.
The current balance type (46) compares the phase current magnitudes and operates when one phase current is significantly different in magnitude from either of the other two phase currents. This is very effective protection for individual motor feeders to detect open phases or unbalances in that circuit.


If other loads are supplied by the circuit to which this protection is connected, care should be taken to ensure that any open phase or unbalance would not be camouflaged by the balanced current to the sound load. One relay should be applied for each load or feeder. The typical minimum sensitivity of these relays is about 1 A in one phase with zero current in the other, or 1.5 pu in one phase and 1 pu in the other.
Another type (46) responds to the negative-sequence current, either instantaneously with a fixed time delay added, or following the I22t = K characteristic, as used for generator protection. These types of relays are not widely applied for motor protection.
As shown in previous section, sufficient V2 voltage is generally available for open phase in the source or upstream system. They should not be applied for open-phase downstream or between the relay and motor, for as indicated, this V2 voltage may be quite low.
When the phases are reversed, 1 pu V1 becomes 1 pu V2, so the negative-sequence relay certainly responds to phase reversals. Phase-reversal relays also are available that are equivalent to a small motor. Normal phase rotation produces restraint or contact-opening torque, whereas phase reversal causes operation or contact-closing torque.
Source: Protective Relaying Principles and Applications by H. Lee Willis and Muhammad H. Rashid











Dear Sir, Hello. We have some problems about axial movement in 6KV electromotor . Please if it is possible; help us to know the cause(s) of this axial movement to solve it. For further information, I should mention that this movement could be seen in the startup of the electromotor (Pump) and after a while (2~3 hours), there would not be any axial movement and then runs normally in rated speed.