Star to Delta Transforms

We can now solve simple series, parallel or bridge type resistive networks using Kirchoff´s Circuit Laws, mesh current analysis or nodal voltage analysis techniques but in a balanced 3-phase circuit we can use different mathematical techniques to simplify the analysis of the circuit and thereby reduce the amount of math’s involved which in itself is a good thing.

Standard 3-phase circuits or networks take on two major forms with names that represent the way in which the resistances are connected, a Star connected network which has the symbol of the letter, Υ (wye) and a Delta connected network which has the symbol of a triangle, Δ (delta).

If a 3-phase, 3-wire supply or even a 3-phase load is connected in one type of configuration, it can be easily transformed or changed it into an equivalent configuration of the other type by using either the Star Delta Transformation or Delta Star Transformation process.

A resistive network consisting of three impedances can be connected together to form a T or “Tee” configuration but the network can also be redrawn to form a Star or Υ type network as shown below.

T-connected and Equivalent Star Network

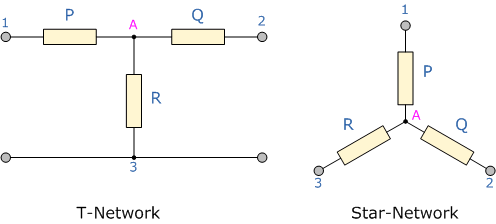
As we have already seen, we can redraw the T resistor network to produce an equivalent Star or Υ type network. But we can also convert a Pi or π type resistor network into an equivalent Delta or Δ type network as shown below.

Reference: Electronics Tutorials