Selecting the suitable frequency converter and motor for these 3 applications

Guidelines for motor selection

The motor is selected according to the basic information about the process. Speed range, torque curves, ventilation method and motor loadability give guidelines for motor selection. Often it is worth comparing different motors because the selected motor affects the size of the frequency converter.

When selecting a suitable frequency converter there are several things to be considered.

Parameters to consider

Frequency converter manufacturers normally have certain selection tables where typical motor powers for each converter size are given.

The dimensioning current can also be calculated when the torque characteristics is known. The corresponding current values can be calculated from the torque profile and compared to converter current limits. The motor’s nominal current gives some kind of indication.

The available supply voltage must be checked before selecting the frequency converter. Supply voltage variations affect the available motor shaft power. If the supply voltage is lower than nominal the field weakening point shifts to a lower frequency and the available maximum torque of the motor is reduced in the field weakening range.

The maximum available torque is often limited by the frequency converter. This has to be considered already in the motor selection phase. The frequency converter may limit the motor torque earlier than stated in the motor manufacturer’s data sheet.

The maximum available torque is also affected by transformers, reactors, cables, etc. in the system because they cause a voltage drop and thus the maximum available torque may drop. The system’s power losses need to be compensated also by the frequency converter rating.

3 applications for frequency converter & motor

1. Pump and fan application
2. Constant torque application
3. Constant power application

1. Pump and fan application

Some stages in pump and fan application dimensioning:

1. Check the speed range and calculate power with highest speed.
2. Check the starting torque need.
3. Choose the pole number of the motor. The most economic operating frequency is often in the field weakening range.
4. Choose motor power so that power is available at maximum speed. Remember the thermal loadability.
5. Choose the frequency converter. Use pump and fan rating. If the pump and fan rating is not available choose the frequency converter according to the motor current profile.

Example //

A pump has a 150 kW load at a speed of 2000 rpm. There is no need for starting torque.

Solution //

The necessary torque at 2000 rpm is T = 9550 × 150 / 2000 Nm = 716 Nm. It seems that 2-pole or 4-pole motors are alternative choices for this application.

1) Motor p=2

For a 2-pole motor the loadability at 2000 rpm according to the loadability curve is about 95 percent. The motor nominal torque must be at least:

T_n ≥ 716 / 0.95 Nm = 754 Nm

The corresponding nominal power must then be at least:

P_n ≥ 754 × 3000 / 9550 kW = 237 kW

2) Motor p=4

For a 4-pole motor the loadability at 2000 rpm is 75 percent. The minimum nominal torque of the motor is:

T_n ≥ 716 / 0.75 Nm = 955 Nm

The minimum power for a 4-pole motor is: P_n ≥ 955 × 1500 / 9550 kW = 150 kW

Go back to contents ↑

2. Constant torque application

Some stages in dimensioning of a constant torque application:

1. Check the speed range.
2. Check the constant torque needed.
3. Check the possible accelerations. If accelerations are needed check the moments of inertia.
4. Check the possible starting torque required.
5. Choose the motor so that torque is below the thermal loadability curve (separate/self ventilation?). Typically the nominal speed of the motor is in the middle of the speed range used.
6. Choose a suitable frequency converter according to the dimensioning current.

Example //

An extruder has a speed range of 300-1200 rpm. The load at 1200 rpm is 48 KW. The starting torque requirement is 200 Nm. Acceleration time from zero speed to 1200 rpm is 10 seconds.

The motor is self-ventilated and the nominal voltage is 400 V.

Solution //

The constant torque requirement is: A suitable motor is a 4-pole or a 6-pole motor.

T = 9550 × 48 / 1200 Nm = 382 Nm

1) Motor p=4

At 300 rpm speed the thermal loadability is 80 percent. The estimated minimum nominal torque is:

T_n ≥ 382 / 0.8 Nm = 478 Nm

The minimum motor nominal power is: P_n ≥ 478 × 1500 / 9550 kW = 75 kW

2) Motor p=6

At speeds of 300 rpm and 1200 rpm the motor loadability is 84 percent. Thus the minimum nominal torque of the 6-pole motor is:

T_n ≥ 382 / 0.84 Nm = 455 Nm

The minimum value of the motor nominal power is:

P_n ≥ 455 × 1000 / 9550 kW = 48 kW

Go back to contents ↑

3. Constant power application

Some stages in dimensioning of a constant power application:

1. Check the speed range.
2. Calculate the power needed. Winders are typical constant power applications.
3. Dimension the motor so that the field weakening range is utilized.

Example //

A wire drawing machine is controlled by a frequency converter. The surface speed of the reel is 12 m/s and the tension is 5700 N. The diameters of the reel are 630 mm (empty reel) and 1250 (full reel). There is a gear with gear ratio n₂ : n₁ = 1 : 7.12 and the efficiency of the gear is 0.98.

Select a suitable motor and converter for this application.

Solution //

The basic idea of a winder is to keep the surface speed and the tension constant as the diameter changes.

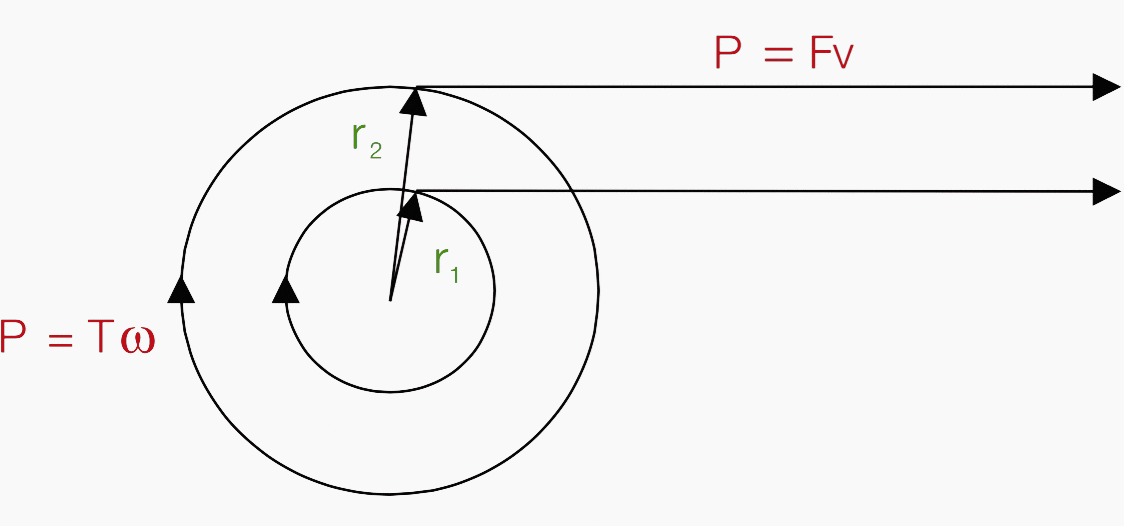
In rectilinear motion the power is: P = Fv
In rotational motion the power is: P = Tω

The relation between surface speed and angular velocity is:

• v [m/s] = (ω × r = 2π × n [rpm] × r) / 60
• n [rpm] = 60 × v / 2π × r
  

Torque is a product of force and radius: T = Fr

By using the above formulas the motor can be selected:

• P = 5700 N × 12 m/s = 68.4 kW
• T₁ = 5700 N × 0.63/2 m = 1796 Nm
• n₁ = 12 × 60 / π × 0.63 rpm = 363.8 rpm
• T₂ = 5700 N × 1.25 / 2 m = 3563 Nm
• n₂ = 12 × 60 / π × 1.25 rpm = 183.3 rpm

The gear must be taken into account before choosing the motor. Speeds, torques and power have to be reduced:

• P = P / η_gear = 68.4 / 0.98 kW = 69.8 kW
• T₁ = (1796 / 0.98) × (1 / 7.12) Nm = 275 Nm
• n₁ = 363.8 × 7.12 rpm = 2590 rmp
• T₂ = (3563 / 0.98) × (1 / 7.12) Nm = 1305 Nm

2) Motor p=2

If a 2-pole motor is selected loadability at a speed of 1305 rpm is about 88 percent and 97 percent at 2590 rpm. The minimum nominal power of the motor is:

P_n ≥ (511 × 3000) / (0.88 × 9550) kW = 182 kW

2) Motor p=4

If a 4-pole motor is selected it can be seen from the loadability curve that loadability at a speed of 1305 rpm is about 98 percent and about 60 percent at 2590 rpm. The minimum nominal power of the motor is:

P_n ≥ (511 × 1500) / (0.98 × 955) kW = 82 kW

Go back to contents ↑

Reference // Dimensioning of a drive system by ABB