
Continued from article Sizing of power cables for circuit breaker controlled feeders (part 2)
3. Criteria Starting and running voltage drops in cable
This criterion is applied so that the cross sectional area of the cable is sufficient to keep the voltage drop (due to impedance of cable conductor) within the specified limit so that the equipment which is being supplied power through that cable gets at least the minimum required voltage at its power supply input terminal during starting and running condition both.
Cables shall be sized so that the maximum voltage drop between the supply source and the load when carrying the design current does not exceed that which will ensure safe and efficient operation of the associated equipment. It is a requirement that the voltage at the equipment is greater than the lowest operating voltage specified for the equipment in the relevant equipment standard.
So before starting with calculation for voltage drop let us first analyze that what is the permissible voltage drop as per relevant standards and guidelines and what is the possible logic behind selecting these values as the permissible values.
Indian standard 1255- CODE OF PRACTICE FOR INSTALLATION AND MAINTENANCE OF POWER CABLES UP TO AND INCLUDING 33 kV RATING in its clause 4.2.3.4 mentions the permissible value for different cross sectional sizes of Aluminium conductor in volts/kM/Ampere for cables from voltage grade of 1.1kV till 33kV. Since we calculate voltage drop in terms of percentage of source voltage, this clause is not very widely used in basic as well as detailed engineering fraternity.
Its complex unit requires to be multiplied by cable length and ampacity. However one can definitely check for any cable size and length, what value is obtained in terms of percentage?
IEEE standard 525 – Guide for the Design and Installation of Cable Systems in Substations in its annexure C, clause number C3 mentions that Voltage drop is commonly expressed as a percentage of the source voltage. An acceptable voltage drop is determined based on an overall knowledge of the system. Typical limits are 3% from source to load center, 3% from load center to load, and 5% total from source to load. These values are indicated diagrammatically below.

dV2 is the drop from load center (PCC) to individual loads which should be less than 3%. Feeder connecting load center to individual loads is also known as secondary feeder.
dV2 = dV1 + dV2 is the total drop from source (Transformer) to load which should be less than or equal to 5%
So far we have understood:
1. What are primary and secondary feeders?
2. What are the permissible values of voltage drop in cables for different types of feeder?
3. What are the governing standards for permissible voltage drop values?
Even though all the electrical equipments are rated for negative tolerance of 10% in voltage, and system voltage variation allowed is also 10% on negative side than why do we design the cable from source to load for a voltage drop of 5% maximum, what is wrong if the cable is also designed for voltage drop of 10%?
Well answer to this lies in the fact that there is a rule of thumb that 2 percent of voltage is lost at terminations and other points like cable joints in a circuit between the power source and the load. Such voltage loss are not indicated and accounted for in cable sizing calculation. The cable sizing calculation only considers the voltage drop in cable conductor from source to load. It is prudent to make certain that the designed voltage drop does not exceed 5% to avoid problems after installation.
It is much more costly to remove and replace an existing cable or piece of equipment that is under rated versus the cost of equipment and cables designed with a degree of extra size and avoid problems due to inadequate voltage at the load.
The NEC recommends or requires a maximum voltage drop of 5%, but realistically connection impedances, deterioration of terminals due to heat and age, etc; add resistance to the total circuit.
Difference between voltage drop and voltage dip?
A voltage dip is a decrease in the magnitude of a supply voltage having the duration of some cycles to seconds. A voltage dip is a power quality problem which occurs due to:
Sudden change in the load, such as suddenly switching ON the large inductive load or any temporary fault in the utility side of the system and impedance of source (Transformer)
Voltage dip is a sort of transient negative side fluctuation of bus voltage which is experienced by all other loads connected to that bus, however it is caused by switching ON of any one single load of large magnitude. It is mainly experienced as a decrease in bus voltage due to starting of large motor. Since bus voltage decreases so other loads connected to that bus experience a fluctuation of voltage. We often come across this phenomenon at our home also when due to sudden switching ON of refrigerator or an air condition the voltage fluctuates.
Even in case of utility the addition of a large load will normally be scheduled with the utility so they can project the time of day that a load, such as an office or industrial plant, is turned on. Whereas the voltage drop is the drop in supply voltage before it reaches to the load. It is totally because of impedance of the connecting cable. It is because of this reason that for checking the adequacy of transformer MVA capacity and suitability of its percentage impedance that we conduct voltage dip calculation after sizing of transformer. Same can also be done by motor starting studies.
Now let us come back to the original topic that is voltage drop and its calculation. As we already know about the permissible values of voltage drop so let us calculate and derive an expression for the same in terms of impedance of cable, cable length and source voltage.
Let us consider a reference phasor as V. Direction of V as X axis and perpendicular to V as Y axis. Approximation OC = OF which is almost equal to OE as EF can be neglected because EF << OF

X component of voltage drop:
= Vdx = AE = AD + DE = AD + BG
= IRCosф + IX Sinф (Equation-1)
Y Component of voltage drop:
= Vdy = CE = CG-EG
= CG-BD
= IXCosф – IRSinф (Equation-2)
X component of VS:
VSx = OE = √ (OC2 –CE2)
VSx = √ VS2 – Vdy2 (Equation-3)
V = OE –AE = VSx – Vdx (Equation-4)
Now Voltage drop Vd is:
Vd = VS – V = VS – (VSx –Vdx) (Putting the value of V from equation-4)
Vd = VS + Vdx – VSx
Vd = VS + Vdx – VS2 – Vdy2 Equation -5 (Putting the value of VSx from equation-3)
Now substituting the values of Vdy and Vdx from equation-2 and equation-1 respectively:
Vd = VS + (IRCosф + IX Sinф) – √ (VS2 – (IXCosф – IRSinф)2 (Equation -6)
Equation-6 is the final expression for voltage drop where:
VS = the supply voltage
I = the load current
R = the resistance of cable conductor in Ohms/kM
X = the reactance of cable conductor in Ohms/kM
The above equation for voltage drop is recommended for exact calculation as per IEEE-241, Recommended Practice for Electric Power Systems in Commercial Buildings, clause number 3.6.1 and IEEE-141, Recommended Practice for Electric Power Distribution for Industrial Plants, clause number 3.11.1
Many consultants recommend the use of above formula for exact calculation of voltage drop in cables meant for power plants. However as per IEEE-525, Guide for the Design and Installation of Cable Systems in Substations, equation number C.2b of Annexure C recommends the use of following formula:
Vd = IRCosф + IXSinф (Equation-7)
Since cable length is usually expressed in meters so before substituting in above expression proper unit conversion should be done.
Sometimes multiple runs of cable are used so number of runs should come as division factor in above expression for equivalent resistance. Multiplying factor of √3 is to be taken for 3 phase system.
That is we are neglecting the vertical component of both the inductive drop and resistive drop. So approximating VS-Vdy almost equal to VS the formula in equation-6 will be reduced to formula in equation-7.
Resistance of cable conductor
Resistance of cable conductor is calculated from resistivity value of conductor material at 20 C, which is a standard temperature for testing adopted by all cable manufacturers. Resistivity is concerted into resistance by following formula:
Rdc = ρ X L / A
Where:
ρ = Resistivity at 20 C
L= 1 kM length
A = Cross sectional area of conductor.
This resistance is DC resistance at 20C. It is converted to DC resistance at 90 C by the following conversion formula:
Rt = R20 (1 + αT)
Where:
R20 = Resistance at 20 C
α = Coefficient of linier expansion of Aluminium
T = Temperature at which resistance is to be calculated
For sizing of cables for AC system the resistance of conductor to be selected should be AC resistance at 90 C and not DC resistance. DC resistance is selected for sizing of cables for DC system like battery, battery charger etc….
A conductor offers a greater resistance to a flow of alternating current than it does to direct current. When the term “ac resistance of a conductor” is used, it means the DC resistance of that conductor plus an increment that reflects the increased apparent resistance in the conductor. This increment is mainly caused by:
Skin effect
This results in a decrease of current density toward the center of a conductor. A longitudinal element of the conductor near the center is surrounded by more magnetic lines of force than is an element near the rim.
Thus, the counter-emf is greater in the center of the element. The net driving emf at the center element is thus reduced with consequent reduction of current density. In simple terms the current tends to crowd toward the outer surface.
Proximity Effect
In closely spaced ac conductors, there is a tendency for the current to shift to the portion of the conductor that is away from the other conductors of that cable. This is called proximity effect. The flux linking the conductor current in one conductor is distorted by the current in a nearby conductor which in turn causes a distortion of the cross-sectional current distribution.
The above mentioned two factors are for increased resistance is generally expressed as the AC/DC resistance ratio. There are other magnetic effects can also cause an additional increase in AC/DC resistance ratios. However we are not going to discuss them in this article. ac/dc ratio is determined by skin effect factor and proximity effect factor.
Rac = (AC/DC) ratio x Rdc
For frequencies higher than 60 hertz, a correction factor for the values of resistance is applied as follows:
x = 0.027678 √ f/Rdc
Where:
f = frequency in hertz
Rdc = conductor DC resistance at operating temperature, in ohms per 1000 feet. The inductance of a multi-conductor cable mainly depends on the thickness of the insulation over the conductor.
Inductive reactance of cable conductor
The inductive reactance of an electrical circuit is based on Faraday’s law. That law states that the induced voltage appearing in a circuit is proportional to the rate of change of the magnetic flux that links it. The inductance of an electrical circuit consisting of parallel conductors, such as a single-phase concentric neutral cable may be calculated from the following equation:
XL = 2π f (0.1404 log S/r + 0.153) x 10-3
Where:
XL = Ohms per 1000 feet
S = Distance from the center of the cable conductor to the center of the neutral
r = Radius of the center conductor
S and r must be expressed in the same unit, such as inches.
Now, in technical articles part-2 and part-1 we had considered the sizing of cable for DOL motor feeder rated at 160kW supplied by 415V. Minimum required area was calculated as 3CX240 Sq mm Al, XLPE, however due to continuous current requirement the cable cross section required was calculated as 3CX300 Sq mm.
Now let us check the running and starting voltage drop for the same using exact equation-6 as well as approximated equation-7.
- Resistance of conductor of 3CX300 mm Sq Al, XLPE cable = 0.128 Ohms/kM (From manufacturers catalog)
- Reactance of conductor of 3CX300 mm Sq Al, XLPE cable = 0.071 Ohms/kM (From manufacturers catalog)
- Cable length = 150Mtr (assumed for this calculation)
- Running power factor of motor = 0.85
- Starting power factor of Motor = 0.3
- Starting current of motor = 6 times rated current
Assuming a drop of 1.5% in the cable for incomer feeder, that is from (source) to load center (PCC) which we have not calculated here for sake of simplicity and space limitation.
Modifying equation-6 for proper units:

L = length of cable = 150 Mtr
N = Number of parallel runs of cable = 1
Substituting the values all the values in the above equation:
Total running voltage drop from source to load = dV1 + dV2 = 1.5% + 2.52% = 4.02% which is < 5%.
Hence total starting voltage drop from source to load = dV1 + dV2 = 1.5% + 11.4% = 12.9% which is < 15%.
Now we can verify the above obtained result by the approximate formula so that we can analyze the amount of approximation involved in using that formula.
Modifying equation-7 for proper units:
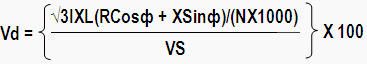
L = length of cable = 150 Mtr
N = Number of parallel runs of cable = 1
Substituting the values all the values in the above equation
Total running voltage drop from source to load = dV1 + dV2 = 1.5% + 2.5% = 4.0% which is < 5%.
Hence total starting voltage drop from source to load = dV1 + dV2 = 1.5% + 11.05% = 12.55% which is < 15%.
Hence we can see that even the approximate formula does give accuracy till one place of decimal and can be used. We can do a small case study by varying the cable length from 50 Mtrs to 150 Mtrs in steps of 15 Mtrs and analyze the difference in voltage drop by the use of two formulas.
| No. | Cable Length | Exact Formula | Approximate Formula | ||
| Running | Starting | Running | Starting | ||
| 1 | 50 | 2.35% | 5.20% | 2.35% | 5.18% |
| 2 | 65 | 2.56% | 6.35% | 2.61% | 6.29% |
| 3 | 80 | 2.80% | 7.47% | 2.86% | 7.39% |
| 4 | 95 | 3.10% | 8.60% | 3.12% | 8.50% |
| 5 | 110 | 3.30% | 9.70% | 3.37% | 9.60% |
| 6 | 125 | 3.63% | 10.00% | 3.63% | 10.70% |
| 7 | 140 | 3.90% | 12.10% | 3.88% | 11.81% |
| 8 | 150 | 4.02% | 12.90% | 4.05% | 12.55% |
Hence we can observer that voltage drop only after one place of decimal as obtained by exact formula is on lesser side where as approximate formula till the route length of 100 Mtrs gives voltage drop on higher side. For route length above 100 Mtrs both the formulas almost converge to give same value of running voltage drop.
Hence it is advisable to go for exact formula as far as possible however the approximate formula also gives the fairly accurate result.
With the completion of third and final criteria of voltage drop we come to the end of sizing of power cables for breaker controlled motor feeders supplied by 415V supply. With this methodology readers can develop a formulated excel sheet for sizing of power cables for circuit breaker controlled feeders.
References:
1. Electrical power cable engineering, edited by William A Thue, Publishers: MARCELD EKKER INC. NEW YORK
2. IEEE Red book
3. IEEE Grey book
4. IEEE-525
5. IEEE-835
6. Indian standard-1255 (second revision)











I have come across a scenario where we are told to do the cable sizing based Steady state voltage with -5% voltage variation. Is this common or recommended in any of the standards.
For eg. LV cable sizing based on 480V(-5% i.e 456V) instead of 480V. Please clarify
Hello,
Thanks for this wonderful article @ the Sizing the cables !
I am confused about the formulas used for DOL starter motors and Star-Delta starter motors i.e., it is @ length.
can we use same formulas DOL starter and Star-Delta starter?
as an example: there is a 30 kW,415 V, 3-ph, 50 Hz motor at a distance of 150 mtr from MCC panel; I want to know the what length used for DOL starter and Star-Delta starter for the calculation of the Voltage Drop – starting+running.
If possible please provide separate formula and help.
Regards,
NILESH
hi dear
thanks for this wonderful article
pl help me in knowing whether voltage drop calculation for 3 ph 3 wire system and 3 ph 4 wire system uses same formulae.
as per IEEE redbook, a single phase system uses multiplying factor 2 and a three phase systemm uses multliplying factor 1.732
the ultimate representation of formula is for 3ph 3wire system converges to the one written by you, however whil calculating for 3ph 4 wire system, is it to be treated as three different single phase ckts and use multiplying factor of 2
pl help.
for more about my question pl refer IEEE redbook 141 page no 113 or Grey Book 241 page 70-75
these describes the derivation of the formula and multiplying factors
and table for voltage drop calcualtion
Dear Mr TK, Your basic doubt is about conversion factors given after table 3-12 of IEEE red book and after table 27 of IEEE grey book. Now the voltage drop formula which I have derived and also given in IEEE is for three phase system and gives line to line drop.
Now there is two more conversion factor given in IEEE which looks to be your concern. Those factors are for:
• Single phase, three wire, line to line
• Single phase, three wire, line to neutral
Before trying to understand this I suggest you to read in totality, table 17 and explanation in grey book and clause 3.1.4 of IEEE red book. Single phase system is of two types:
Single phase two wire (which is derived from 3 phase 4 wire system) this system is widely used everywhere. In India and other places domestic supply has only one standard voltage level of 240V. So voltage between phase and neutral is 240V and this system is basically called single phase two wire. A third wire is also seen in this system which is earth but this earth is external safety earth and not system earth hence this system is called single phase two wire and not single phase three wires.
Single phase three wires which is mainly used as North American residential supply system. In this system the secondary winding of the supply transformer is center tapped and earthed, providing the neutral, while opposite ends of the secondary winding provide the two line conductors. Loads connected between the line conductors are at 230V, whereas loads connected between any of line conductor and the neutral are at 120 V. Do not mistake this with a two phase system. if two phases from a three phase system are taken then with the neutral included this would be a two phase system as the two line wire are not in phase with each other so there are truly two phases. If however a center tap is taken as a neutral from a single winding of a transformer feed with two phases then the two outputs are in phase and it can be called as split phase.
Now let us consider the voltage relationship between above defined system.
1. Three phase line to line voltage=V
2. Three phase line to neutral voltage= V/√3= Single phase 2 wire line to neutral voltage= Single phase 3 wire line to line voltage
3. Single phase 3 wire line to line voltage = V’
4. Single phase 3 wire line to neutral voltage = V’/2
Now considering the above relationship let us come back understand the conversion factors given in IEEE.
• Voltage drop for 3 phase line to line is= x than as per equation-2 the voltage drop for 3 phase line to neutral will be x/√3 or 0.577 times x hence the conversion factor 0.577
• Voltage drop for 3 phase line to line is= x than as per equation-2 the line to line voltage drop for single phase, 3 wire system will be= 2x/√3 hence the conversion factor 1.15 (for extra 2 please note that circuit length will get doubled, please diagrammatically analyze the circuit for load connected across line in a single phase 3 wire system)
• Voltage drop for single phase, 3 wire system line to line is= 2x/√3 than as per equation-3 & 4 the line to neutral voltage drop will be (2x/√3)/2= x/√3 hence the conversion factor 0.577. Also please note that for perfectly balanced load connected between line1 and neutral and line 2 and neutral of single phase 3 wire system this is true as there will not be any current through neutral. However for unbalance loads between line-1 and line-2 and neutral this drop will be more and will depend on degree of unbalance and in worst case can become equal to single phase three wire line to line drop.
I hope this clarifies your concern. However I suggest that the other two conversion factors for Single phase, three wire, line to line and single phase, three wires, line to neutral is not of much practical utility for design engineer practicing in Asia or Europe where there is only one single phase domestic supply of 240V. For 3 phases 4 wire system please do not consider it as three different single phase circuit the 3 phase line to line voltage drop will remain same.
Your other doubt is related to conversion factor given in page 97 of red book. Conversion factor of 2 is given for single phase and 1.732 is for 3 phase is your other doubt. Please note that IEEE simply means here that line to neutral voltage drop for three phase system or per phase voltage drop in three phase system has to be multiplied by 2 (circuit length getting doubled) and by 1.732 for line to line voltage drop.
First and foremost, your article was very very thorough. I went through your entire article and cannot get the answers that you got in your comparison. The modified equation 7 seems to have an extra X in it. However, the Exact modified formula I cannot get the same values as you and I cant figure out why. I started on this quest because ETAP and SPEL were sizing cables 2 cable sizes off. I realized that SPEL uses a simplified formula that assumes that the imaginary axis component of the voltage is very small compared to the real axis. I wonder if you could double check the exact formula to make sure it is right. Thanks for the article it really helped me!
Dear Mr Maswist thanks a lot for the careful observation……………….the extra X which you are talking about is actually IXL (Current multiplied by length) as in denominator NX1000 (number of runs multiplied by 1000) however as a representation mistake it has been represented similar to inductance X as in XSin(phi).
Thanks for sharing your experinces.
As I told you before, thank you for sharing your expirience. It’s not an easy task to put your expirience in words and pictures.
Thank you for sharing a lot of industrial experience here. Thumb up to the contributor!