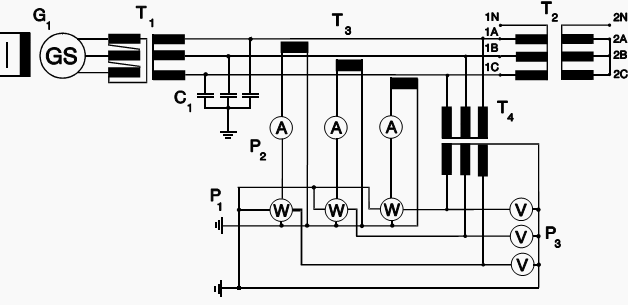
Purpose of the measurement
The measurement is carried out to determine the load-losses of the transformer and the impedanse voltage at rated frequency and rated current.
Apparatus and measuring circuit
On Figure 1 above (Circuit for the impedance and load-loss measurement) there are following figures:
- G1 – Supply generator
- T1 – Step-up transformer
- T2 – Transformer to be tested
- T3 – Current transformers
- T4 – Voltage transformers
- P1 – Wattmeters
- P2 – Ammeters (r.m.s. value)
- P3 – Voltmeters (r.m.s. value)
- C1 – Capacitor bank
The supply and measuring facilities are not described here. Current is generally supplied to the h.v. winding and the l.v. winding is short-circuited.
Performance of the measurement
If the reactive power supplied by the generator G1 is not sufficient when measuring large transformers, a capacitor bank C1 is used to compensate part of the inductive reactive power taken by the transformer T2.The voltage of the supply generator is raised until the current has attained the required value (25…100 % of the rated current according to the standard 4.1).
In order to increase the accuracy of readings will be taken at several current values near the required level. If a winding in the pair to be measured is equipped with an off-circuit or on-load tap-changer. the measurements are carried out on the principal and extreme tappings.
It the transformer has more than two windings all winding pairs are measured separately.
Results
Corrections caused by the instrument transformers are made to the measured current, voltage and power values. The power value correction caused by the phase displacement is calculated as follows:

Where:
- Pc = corrected power
- Pe = power read from the meters
- δu = phase displacement of the voltage transformer in minutes
- δi = phase displacement of the current transformer in minutes
- ϕ = phase angle between current and voltage in the measurement (ϕ is positive at inductive load)
- K = correction
The correction K obtained from equation 4.1 is shown as a set of curves in Figure 4.2.
The corrections caused by the instrument transformers are made separately for each phase, because different phases may have different power factors and the phase displacements of the instrument transformers are generally different.
If the measuring current Im deviates from the rated current IN, the power Pkm and the voltage Ukm at rated current are obtained by applying corrections to the values Pc and Uc relating to the measuring current.
The corrections are made as follows:
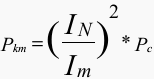
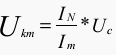
The correction caused by the phase displacement of instrument transformers (Figure 2):

Where:
- K – correction in percent,
- δu – δi – phase displacement in minutes
- cosδ – power factor of the measurement.
The sign of K is the same as that of δu – δi.
Mean values are calculated of the values corrected to the rated current and the mean values are used in the following. According to the standards the measured value of the losses shall be corrected to a winding temperature of 75° C (80° C, if the oil circulation is forced and directed).
The transformer is at ambient temperature when the measurements are carried out. and the loss values are corrected to the reference temperature 75° C according to the standards as follows.
The d.c. losses POm at the measuring temperature ϑm are calculated using the resistance values R1m and R2m obtained in the resistance measurement (for windings 1 and 2 between line terminals):
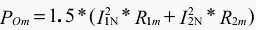
The additional losses Pamat the measuring temperature are:

Here Pkm is the measured power, to which the corrections caused by the instrument transformer have been made, and which is corrected to the rated current according to equation (4.2).
The short-circuit impedance Zkm and resistance Rkm at the measureing temperature are:

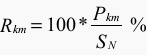
- Ukm is the measured short-circuit voltage corrected according to Equation (4.3);
- UN is the rated voltage and
- SN is the rated power.
The short circuit reactance Xk does not depend on the losses and Xk is the same at the measuring temperature (ϑm) and the reference temperature (75 °C), hence:
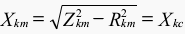
When the losses are corrected to 75° C, it is assumed that d.c. losses vary directly with resistance and the additional losses inversely with resistance. The losses corrected to 75° C are obtained as follows:
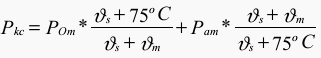
Where:
ϑs = 235° C for Copper
ϑs = 225° C for Aluminium
Now the short circuit resistance Rkc and the short circuit impedance Zkc at the reference temperature can be determined:

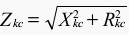
Results
The report indicates for each winding pair the power SN and the following values corrected to 75° C and relating to the principal and extreme tappings.
- D.C. losses POc (PDC)
- Additional losses Pac (PA)
- Load losses Pkc (PK)
- Short circuit resistance Rkc (RK)
- Short circuit reaactance Xkc (XK)
- Short circuit impedance Zkc (ZK)
Reference: Testing of power transformers – ABB











Please help me calculate copper looses…I want to specify a high impedance value for transformers to reduce the fault level. I however established that this compromises/degrades the stability of the system/network and that there are high copper losses which may results into higher tariffs….please help me understand this.
Good Morning,
I like this site. it really help a lot.
I also need assistance. I have a very old transformer with a transformer nameplate invisible. I would like to know if is there any other way of calculating an estimated voltage impedance without using the standard transformer impedance measurement as indicated above using:
On Figure 1 above (Circuit for the impedance and load-loss measurement) there are following figures:
G1 – Supply generator
T1 – Step-up transformer
T2 – Transformer to be tested
T3 – Current transformers
T4 – Voltage transformers
P1 – Wattmeters
P2 – Ammeters (r.m.s. value)
P3 – Voltmeters (r.m.s. value)
C1 – Capacitor bank
Is there any other way to calculate this?
Hi i would like to call you in person in regsrds to testing of distribution transformers .
In the process of starting a manufacturing facility in Australia.
Thank you
Sir explain to movementing parallel operation of swithgear system
Send me latest electrical news.
Thanks for newsletter!
I m nt a engineer nw, bt nw its too good.reading articles by you