The quality of energy systems
Reactive energy compensation is an essential process in improving energy efficiency. It reduces the power consumption and thus its cost, enables optimum use of installations by preventing them being oversized, and more generally it improves the quality of energy systems.

- Introduction to reactive energy
- Parallel RLC Circuit
- Current diagram
- Power diagram
- Use of the tangent φ
1. Introduction to reactive energy
Inductive loads, typically motors and transformers, and also certain types of lighting with ballast, as well as welding equipment or induction heating, have the particular feature of operating with the help of a magnetic field. Some of the power needed to generate this magnetic field is not converted into heat or work.
Very long lines (by inductive storage) and also static converters (controlled rectifiers, Ac power controllers, etc.) can also consume unnecessary energy by phase-shifting the current behind the fundamental voltage.
Unlike the compensation of inductive circuits, compensation of predominantly capacitive circuits requires the use of inductances to absorb the reactive energy that is produced.
This situation is found on distribution circuits (very long lines, cable networks), often when there is a low load on the circuits. new installations that use numerous electronic power supplies (data centres) may also have this particular feature.
As well as avoiding feeding the energy back onto the system, compensation of an installation with too high a capacitance is necessary to limit the transient overcurrents and overvoltages that could occur when such loads are switched on, and to avoid self-excitation of synchronous motors.
The harmful consequences of reactive power on transmission lines described previously is also found in installations:
- It increases the necessary current at the risk of causing destructive overcurrents and problematic voltage drops leading to the need to oversize the conductors.
- It reduces the available active power, which limits the possibilities of using the source or requires it to be oversized.
- It generates an additional operating cost connected with the pricing of the reactive energy consumed and measured by the distribution company.
1.1 Over-compensation
Over-compensation (Ic >Ir) increases the apparent current consumed and also increases the voltage applied to the equipment. The illustration of vectors V2S (with over-compensation) and V2 (with appropriate compensation) shows this phenomenon, which must be avoided.
Care must be taken when choosing energy compensation.


2. Parallel RLC Circuit
Industrial systems are generally parallel RLC circuits. However each branch may itself make up other complex series or series/parallel systems. All three elements share the same supply voltage.
The total current it is equal to the vectorial sum of the currents of all three elements: it = iR + iL + iC


The impedances of the inductive, resistive and capacitive branches of the circuit are respectively:
ZL = Lω
ZR = R
ZC = –1/Cω
The impedance of this type of circuit is equal to the inverse of the sum of the inverses of each impedance:
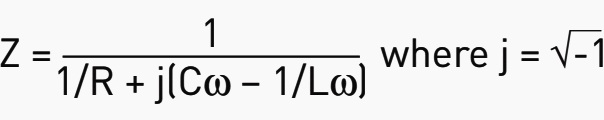
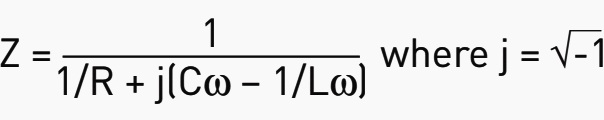
This equation shows that the impedance part due to the capacitance and the inductance may tend towards 0 if Lω = -1/cω. This is the phenomenon of resonance (or more precisely, anti-resonance, as UL and UC are in anti-phase) which occurs at certain frequencies corresponding to an angular frequency:


Due to the equality Lω = –1/cω, the impedance of the circuit is reduced at the resistive branch R. the current may then suddenly increase to dangerous or even destructive values.
The power of each branch is written as follows:
- PR = IR2 × R
- QL = IL2 × Lω
- QC = IC2 × (1/cω)
3. Current diagram
The phase shifts between currents in parallel RLC circuits and the powers associated with each of the impedances that make up these circuits can be represented by Fresnel current and power diagrams, which show the concepts of phase shift (ϕ) and power factor (PF or λ).
The power factor characterises the ratio of the active (useful power) power to the apparent power (sum of the active power and the reactive power).
When the currents and voltages are totally sinusoidal, the current diagrams and power diagrams are similar and the power factor (PF or λ) is identical to the cosine ϕ of the displacement angle between the U and I vectors.
3.1 Inductive circuit
The below current diagram can be used to locate the vectors representing each of the three components of a parallel RLC circuit.

Where:
- IR is current in the resistive branch
- IL is current in the inductive branch
- IC is current in the capacitive branch
- It is total apparent current
The voltage u of the source is considered to be the reference. It should be noted that in this example, the value of IL (reactive current in the inductance) is greater than that of IC (reactive current in the capacitance). The ϕ angle is negative.
Adding capacitors will thus make it possible to supply the reactive current necessary for the compensation of IL.
The following relationships are established based on this diagram:
- Ia = It × cosϕ (active current),
- Ir = It × sin ϕ (reactive current),
- It² = Ia2 + Ir2 (apparent current).
3.2 Capacitive circuit
In the diagram below, the value of IC (reactive current in the capacitance) is greater than that of IL (reactive current in the inductance) and the ϕ angle is positive.
To compensate for the reactive current IC being too high, shunt reactors must be used. This must not be confused with the insertion of inductances in series with the capacitors, which is intended to limit the risk of resonance.


The 2nd diagram is a simplified representation that is often used, in which the sum of IL and IC is written Ir (for reactive).
If there are non-linear loads an additional power, referred to as distorting power, is introduced and the equality of the ratios between the power and the sinusoidal currents is no longer verified.
Only measurement of the power rms values will give the power factor.
3.3 Groups of loads
Additivity of reactive powers installations are made up of numerous groups of loads connected in parallel (A, B, C, etc. in the example below).


The current/voltage phase shift and the total current it consumed by these groups of loads are the result of adding the current vectors. This is a somewhat complicated mathematical approach.
However, the reactive power is easy to calculate from the arithmetical sum of the various powers of each load:
- Receiver A is made up of inductance L1 and resistor R1,
- Receiver B is made up of inductance L2 and resistor R2.
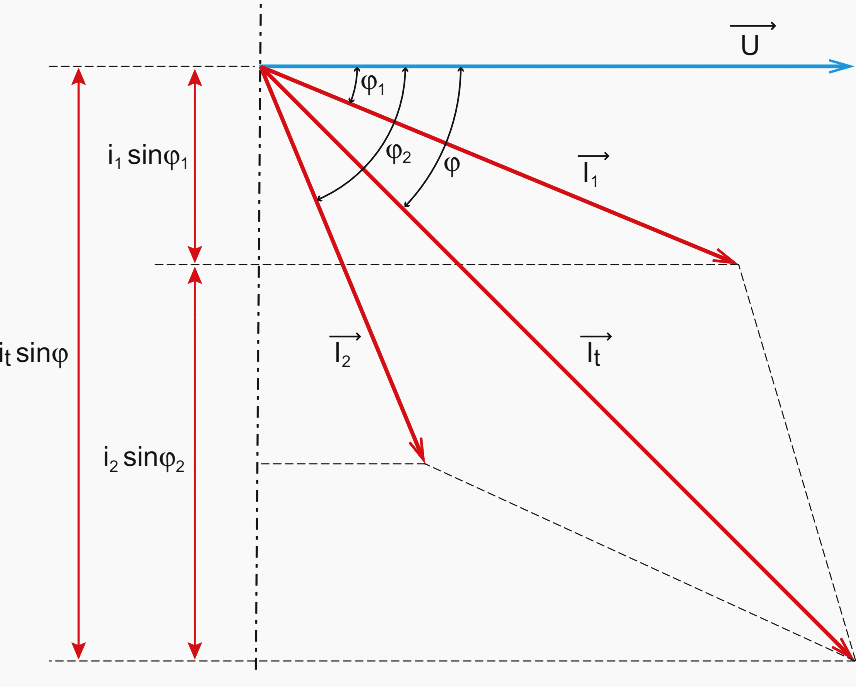

The Fresnel diagram of the group of receivers A and B demonstrates the relationship between vectors It, I1 and I2 associated with the sinusoidal values it, i1 and i2 respectively:
It × sin ϕ = I1 × sin ϕ1 + I2 × sin ϕ2
Multiplying the two members of the equation by U (common voltage in parallel group), gives:
U × It × sin ϕ = U × I1 × sin ϕ1 + U × I2 × sin ϕ2
The reactive power of the group of receivers is equal to the sum of the reactive powers of each receiver, i.e. Q = Q1 + Q2
This rule, which can be generalised to any group of receivers supplied with the same sinusoidal voltage is known as Boucherot’s theorem (Q = ΣQn).
4. Power diagram
The two representations above are possible as the power has no sign. however, and by analogy with the current diagram, the first representation is preferable.


Where:
- P = U × I × cos ϕ (active power in kW)
- Q = U × I × sinϕ (reactive power in kvar)
- S = U × I × (apparent power in VA)
For linear loads:
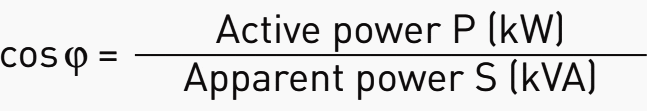
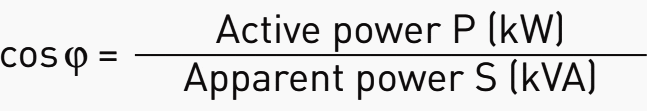
5. Use of the tangent φ
The tangent ϕ characteristic is widely used for its practicality. The closer it is to zero the less reactive energy is consumed. The advantage of this expression is that it characterizes the balance of the exchange of reactive energy between the supply source and the consuming installation.
Thus, if the power compensation is too high, the reactive power Q becomes positive again and the tangentϕ once again moves away from zero.


The permitted values for tanϕ vary according to the country and the supply contract. For example, in France, the value above which billing is triggered (according to tarif period) is 0.4 (corresponding to a cos of 0.93) seen from the High Voltage metering side, which also incorporates the reactive consumption of the connection transformer.
The separation of electrical energy transmission and distribution companies leads to consideration of the possibility of lowering the tan value to 0.2.
The search for additional savings by penalizing the reactive energy comes up against the technical requirement of reducing the resonance frequency of installations caused by too many capacitors.
These are all contradictory elements that show that it is important to have a good knowledge of the characteristics of the installation and its receivers when implementing any compensation project.
Source: Electrical energy supply by Legrand










correct tg = Q/P
5. Use of the tangent φ
Tan φ = Q (kVAr)/ P(kW)
= sqrt (S@2 – P^2) / P
= [U x I x sqrt(1 – cos(φ)^2)] / [U × I × cos ϕ]
= sqrt(1- cos(φ)^2) / cos(φ)
Thus, the first equation of tan φ is wrong, however the second one is correct.
Please fixed it.
EEP articles and write ups are very informative 👌
Tan£ its wrong
The correct form is Tan£=Q/P