Where and Why Do We Use Phase-Shifting Transformers?

Basic Principle of Application

Because of the predominantly inductive character of the power system, an active power flow between source and load must be accomplished with a phase lag between the terminals. Phase-shifting transformers are a preferred tool to achieve this goal.

Two principal configurations are of special interest:

1. The power flow between transmission systems operating in parallel where one system includes a PST and
2. Where a single transmission line which includes a PST is connecting two otherwise independent power systems.

The latter is in fact a special case of the first, but it has become more important nowadays for the interconnection of large systems. For the following considerations, it is assumed that the ohmic resistance R is small compared with the reactance X and thus has been neglected.

Situation – One practical basic situation is that a location where power is needed (load side) is connected to the source side through two systems that need not necessarily have the same rated voltage level.

See Figure 1 below.

Without any additional measure, the currents I₁ and I₂ would be distributed in proportion to the ratio of the impedances of the systems,

I₁ = I × X₂/(X₁ + X₂)
I₂ = I × X₁/(X₁ + X₂)

and there is no doubt that system 2 would take only a small part of the load because of the additional impedances of the two transformers in that branch.

Presuming that active power should be supplied to the load side and considering the inductive character of the systems, this voltage must have a 90° phase lag to the line-to-ground voltages of the system (V_L).

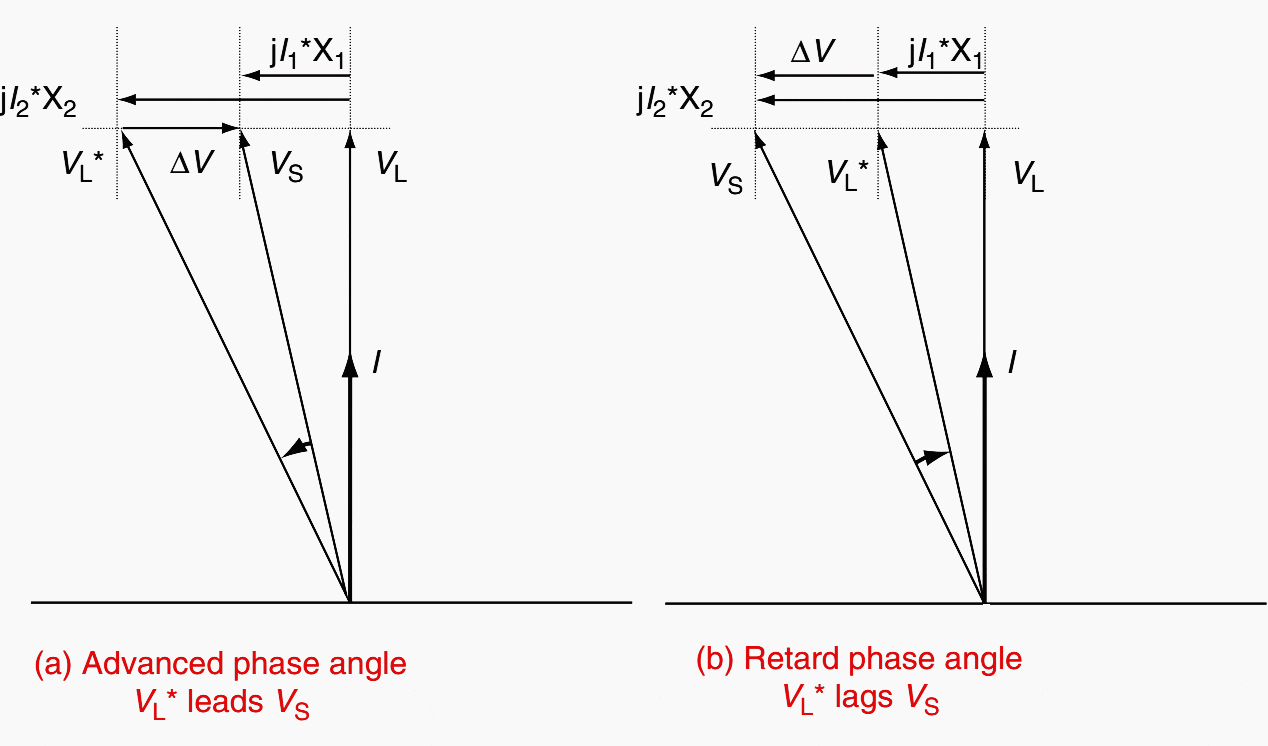
In principle, the source of ΔV could be installed in each of the two systems. Figure 2 shows the voltage diagrams of both options. Figure 2a corresponds to Figure 1 with the PST installed in system 2, the system with the higher impedance. The additional voltage reduces the voltage drop in system 2 to that of system 1.

The voltage at the output or load side of the PST V_L* leads the voltage at the input or source side VS. Per definition, this is called an advanced phase angle. If the PST were installed in system 1 (Figure 2b), the additional voltage would increase the voltage drop to that of system 2.

In this case, the load-side voltage V_L* lags the source side voltage V_S, and this is defined as retard phase angle. As can also be seen from the diagrams, an advanced phase angle minimizes the total angle between source and load side.

The second important application is the use of a PST to control the power flow between two large independent grids (Figure 3). An advanced phase angle is necessary to achieve a flow of active power from system 1 to system 2.

Types of Phase-Shifting Transformers

General Aspects

The general principle to obtain a phase shift is based on the connection of a segment of one phase with another phase. To obtain a 90º additional voltage ΔV, the use of delta-connected winding offers the simplest solution.

The phasor diagram has been plotted for no-load conditions, i.e., without considering the voltage drop in the unit. It also should be noted that the currents in the two halves of the series winding are not in phase.

This is different from normal power transformers and has consequences with respect to the internal stray field.

V_S1 = V₁₀ + (ΔV₁/2)

V_L1 = V₁₀ − (ΔV₁/2)

ΔV₁ = V_S1 −V_L1

From the phasor diagram (Figure 4b) follows (V_S1 = V_L1 = V):

V₀ = V × cos(α/2)

ΔV = V × 2 × sin(α/2)

V_Δ = V × cos(α/2) × √3

and with I_S = I_L = I, the part of the current that is transferred to the exciting winding becomes:

I_Δ = (ΔV/V_Δ) × I × cos(α/2) = I × (2/√3) × sin(α/2)

The throughput power can be calculated from

P_SYS = 3 × V × I

and the rated design power, which determines the size of the PST, becomes

P_T = 3 × ΔV × I = P_SYS × 2 × sin(α/2)

In two-core designs (Equation ΔV₁ = V_S1 −V_L1), this power determines also the necessary breaking capability of the OLTC.

P_Δ = V_Δ × I_Δ = 1/3 × P_SYS × sin(α)

In addition to the transferred power, the phase-shift angle is also important.

In the optimum case when the load power factor is close to 1, a PST impedance of 15% would reduce the load phase-shift angle by 8.58.

In practice, various solutions are possible to design a PST. The major factors influencing the choice are:

1. Throughput power and phase-shift angle requirement
2. Rated voltage
3. Short-circuit capability of the connected systems
4. Shipping limitations
5. Load tap-changer performance specification

In addition, preferences of a manufacturer as to the type of transformer (core or shell) or type of windings and other design characteristics may also play a role.

Depending on the rating, single- or two-core designs are used. Two-core designs may require either a one-tank or a two-tank design.

Single-Core Design

Symmetrical conditions are obtained with the design outlined in Figure 4a. Figure 5a and Figure 5b show the general connection diagrams with more details of the regulating circuit.

The advantage of the single-core design is simplicity and economy. But there are also a number of disadvantages.

The advantage of the symmetrical design (Figure 5a) is that the phase-shift angle is the only parameter that influences the power flow. The design needs two single-phase OLTCs (for low ratings, one two-phase OLTC may be used instead) per phase or two three-phase OLTCs.

Figure 5b shows an unsymmetrical solution. Only one-half of the regulating windings is used. The number of necessary OLTCs is reduced, but the ratio between source voltage and load voltage changes with the phase-shift angle and additionally influences the power flow.

A solution that often is used for transformers interconnecting two systems is shown in Figure 6.

The tap winding of a regulating transformer can be connected to a different phase, causing a voltage shift between the regulated winding and the other windings of the unit.

The regulated winding normally is connected to the source side, but indirect regulation of the load-side is also possible. The change from the normal regulating transformer state to the phase-shifting state is possible in the middle position of the OLTC without the need to switch off the unit.

Another solution of a symmetrical PST, the delta-hexagonal phase-shifting transformer, is shown in Figure 7.

Two-Core Design

The most commonly used circuit for a two-core design is shown in Figure 8 below. This configuration consists of a series unit and a main unit. For smaller ratings and lower voltages, two-core PSTs can be built into a single tank, while larger ratings and higher-voltage PSTs require a two-tank design.

Since OLTCs have limited current ratings and step voltages per phase as well as limited switching capacity, they are the main limiting features for the maximum possible rating of PSTs. More than one OLTC per phase may have to be utilized for very large ratings.

Up to a certain rating, three-pole OLTCs can be used. For higher ratings, three single-pole OLTCs are necessary. The OLTC insulation level is independent of the system voltage and can be kept low. The short-circuit impedance is the sum of the impedances of the main and series transformers.

Because the impedance of the series unit is constant and independent from the phase angle, the unit can be designed to be self-protecting, and the variation of the impedance with the phase-shift angle can be kept small when the impedance of the main unit is kept low.

Quadrature Booster Transformers

Quadrature booster transformers are a combination of a regulating power- or auto-transformer with a phase-shifting transformer. The PST, which can be a single- or two-core design, is supplied from the regulated side of the power transformer (Figure 9).

By this method, the output voltage can be adjusted in a four-quadrant (magnitude and phase) relationship.

Reference // Electric Power Engineering Handbook by Leonard L. Grigsby (Purchase hardcopy from Amazon)