Techniques for solving DC circuits
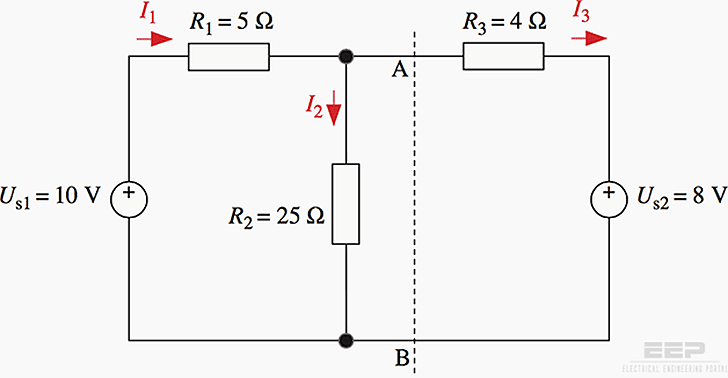
Referring to the following circuit, calculate direct current I3:
- Using Kirchhoff’s laws;
- Using nodal analysis;
- Applying Thévenin’s theorem at nodes A and B.
Ok, let’s dive into calculation…
Kirchhoff’s Current Law – The algebraic sum of currents at a node is zero.
Kirchhoff’s Voltage Law – The algebraic sum of voltages around a closed circuit loop is zero.
– KCL stands for Kirchhoff’s Current Law
– KVL stands for Kirchhoff’s Voltage Law
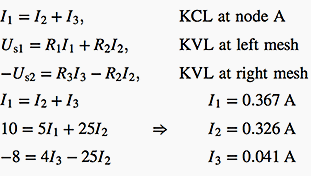
The following equation can be written:
![]()
Substituting values, we obtain:

Finally,

Thévenin’s voltage UTh at nodes A and B can be easily calculated by disconnecting the right part of the circuit:
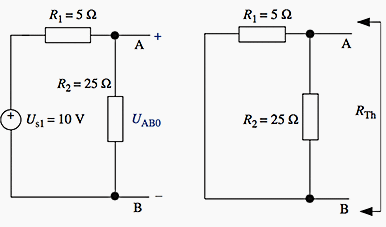
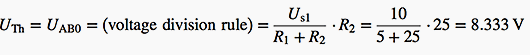
Thévenin’s equivalent resistance RTh is the resistance “seen” from nodes A and B, when all generators are deactivated (in our case, only E1 is present):
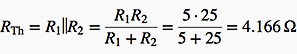
The left side of the circuit can now be substituted by its Thévenin equivalent, in order to calculate current I3:
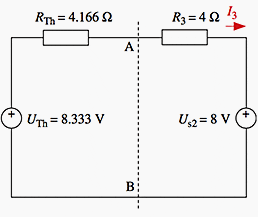
This single-mesh circuit can be easily solved using KVL (Kirchhoff’s voltage law):
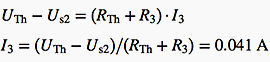
Readers should note that UAB0 ≠ UAB:
UAB = UTh – RTh · I3 = 8.333 – 4.166 · 0.041 = 8.163
Comparing the three methods, we can conclude that Thévenin’s theorem is very powerful, in particular when a single current value is needed.
Another Kirchhoff’s Laws Worked Example (VIDEO)
Thevenin’s Theorem. Example with solution (VIDEO)
Reference // Fundamentals of electric power engineering – Ceraolo, Massimo, Davide Poli.











I want more information about electrical engineering.
Nostalgic knowledge
Very good materials for Electrical Engineering practice.