4 example calculations of compensation for reactive power

Reactive power

First, let’s say some words about basics of the reactive power in system. Reactive current arises in every electrical system. Not only large loads, but smaller loads as well require reactive power. Generators and motors produce reactive power, which causes unnecessary burdens to and power losses in the lines.

Figure 1 shows the block diagram for the network loading.

Reactive power is necessary to generate magnetic fields, e.g. in motors, transformers and generators. This power oscillates between the source and the load and represents an additional loading.

Now, let’s take few examples to calculate the following:

1. Determination of Capacitive Power
2. Capacitive Power With k Factor
3. Determination of Cable Cross-Section
4. Calculation of the c/k Value

Example 1 – Determination of Capacitive Power

A load has an effective power of P = 50 kW at 400 V and the power factor is to be compensated from cosφ = 0.75 to cosφ = 0.95. Determine the required capacitive power. The power and current before compensation are:

The power and current after compensation are:

The required capacitive power  is:

Go back to calculations ↑

Example 2 – Capacitive Power With k Factor

The capacitive power can be determined with the factor k for a given effective power. The k factor is read from a table 1 – Multipliers to determine capacitor kilovars required for power factor correction (see below) and multiplied by the effective power. The result is the required capacitive power.

For an increase in the power factor from cosφ = 0.75 to cosφ = 0.95, from the table 1 we find a factor k = 0.55:

Go back to calculations ↑

Example 3 – Determination of Cable Cross-Section

A three-phase power of 250 kW, with Un = 400 V, at 50 Hz is to be transmitted over a cable 80 m in length. The voltage drop must not exceed 4% =16 V. The power factor is to be increased from cosφ = 0.7 to cosφ = 0.95. What is the required cable cross-section?

The current consumption before compensation is:

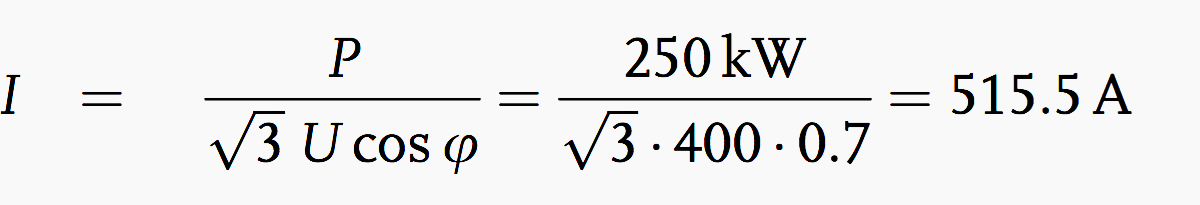
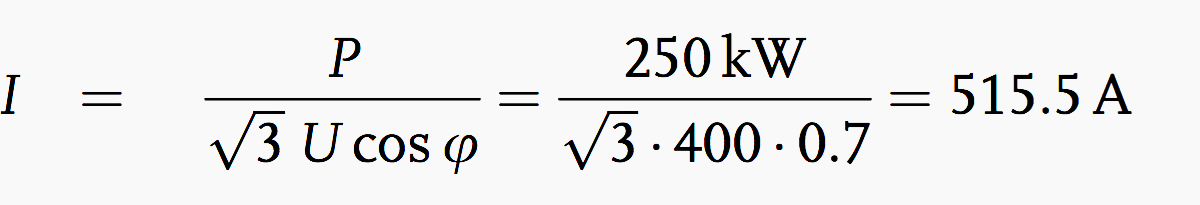
The current consumption after compensation is:

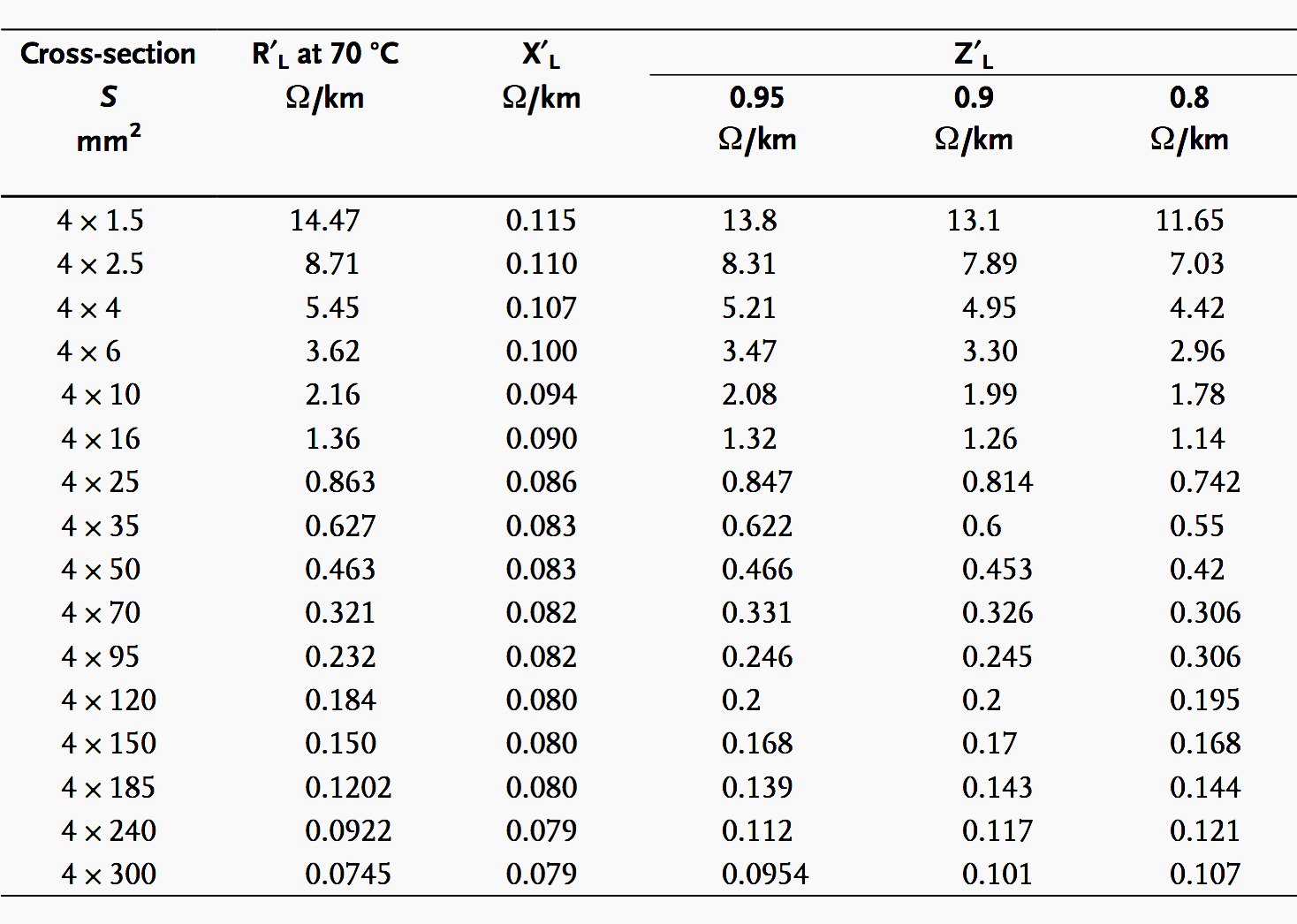
The effective resistance per unit length for 516 A is:

According to Table 2 (see below) we must choose a cable with a cross-section of 4 × 95 mm². The effective resistance per unit length for 380 A is:

Go back to calculations ↑

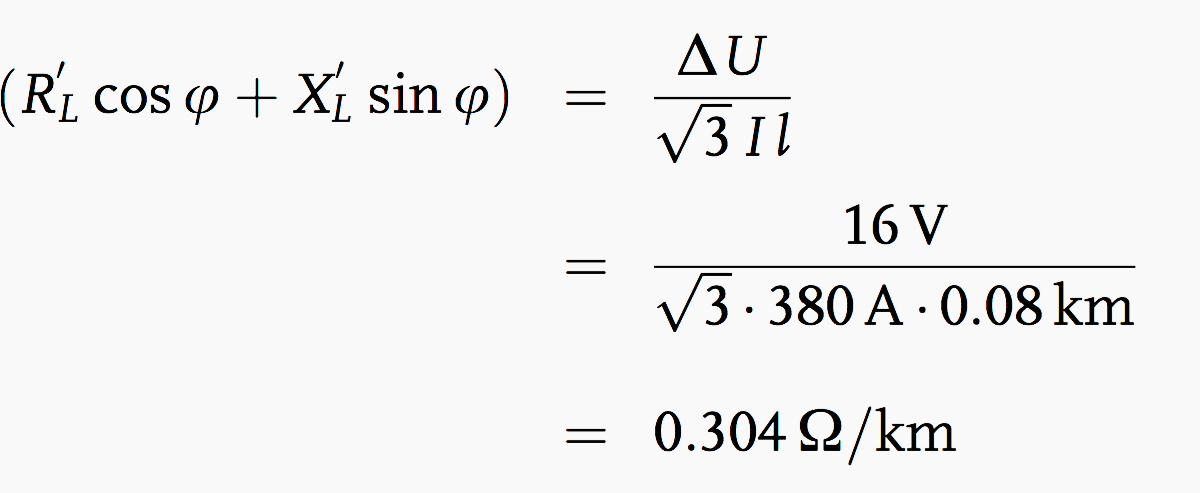
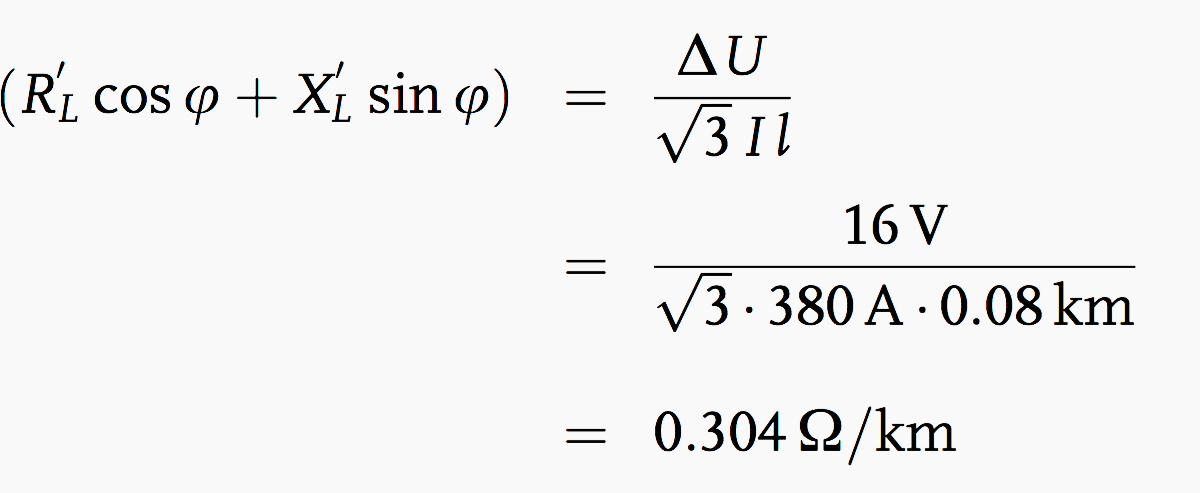
Example 4 – Calculation of the c/k Value

Given a 150 condenser battery, i.e. 5 stages of 30 each, a supply voltage of 400 V, and an instrument transformer with a k of 500 A/5 A, how large is the c/k value? The ratio c/k is given by.

Go back to calculations ↑

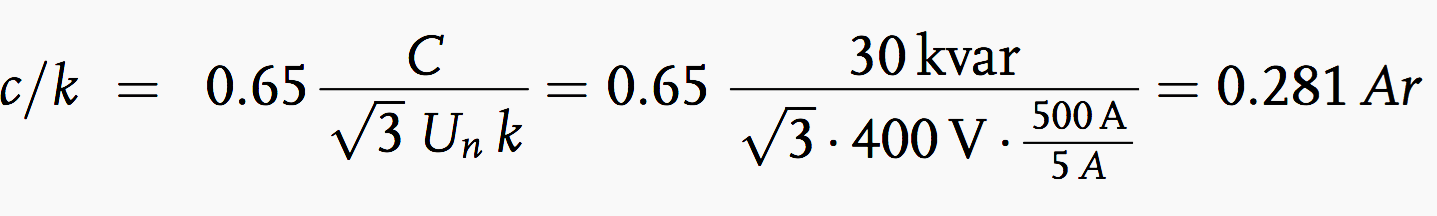
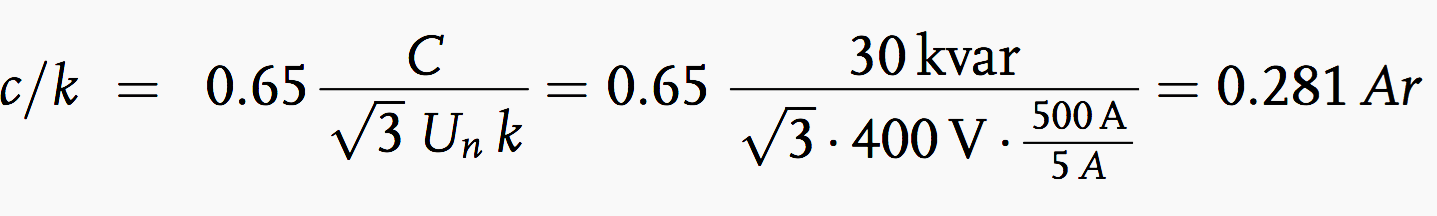
Tables

Table 1 – Multipliers to Determine Capacitor Kilovars Required for Power Factor Correction

Table 2 – Resistance per unit length for (Cu) cable with plastic insulation

Go back to calculations ↑

References

1. Analysis and design of low voltage power systems by Ismail Kasikci (Purchase hardcover from Amazon)
2. Power factor correction – A guide for the plant engineer by EATON