Network analysis
This guide will introduce the important fundamental theorems of network analysis. Included are the superposition, Thévenin’s, Norton’s, maximum power transfer, substitution, Millman’s, and reciprocity theorems. We will consider a number of areas of application for each. A thorough understanding of each theorem is important because a number of the theorems will be applied repeatedly in the material to follow.

Superposition Theorem
The superposition theorem, like the methods of the last chapter, can be used to find the solution to networks with two or more sources that are not in series or parallel. The most obvious advantage of this method is that it does not require the use of a mathematical technique such as determinants to find the required voltages or currents.
Instead, each source is treated independently, and the algebraic sum is found to determine a particular unknown quantity of the network.
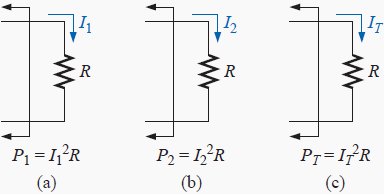
The current through, or voltage across, an element in a linear bilateral network is equal to the algebraic sum of the currents or voltages produced independently by each source.
When one is applying the theorem, it is possible to consider the effects of two sources at the same time and reduce the number of networks that have to be analyzed, but, in general,
Number of networks to be analyzed = Number of independent sources
To consider the effects of each source independently requires that sources be removed and replaced without affecting the final result.
To remove a voltage source when applying this theorem, the difference in potential between the terminals of the voltage source must be set to zero (short circuit); removing a current source requires that its terminals be opened (open circuit).
Any internal resistance or conductance associated with the displaced sources is not eliminated but must still be considered.
| Title: | Network Theorems |
| Format: | |
| Size: | 610.7 KB |
| Pages: | 54 |
| Download: | Here 🔗 (Get Premium Membership) | Video Courses | Download Updates |
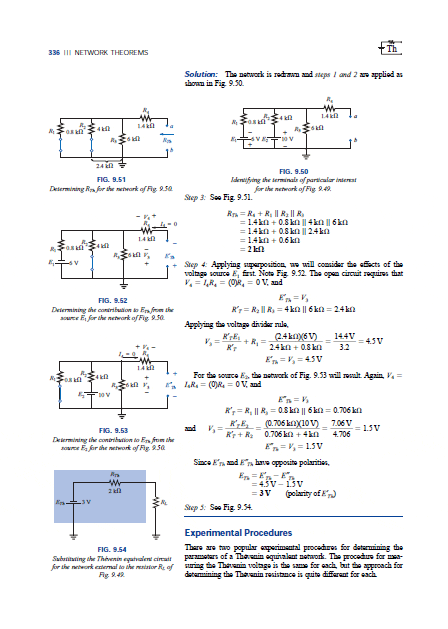


what book is your source here? thank you