Penalties? Money lost?
Power supply authorities apply a tariff system which imposes penalties on the drawing of energy with a monthly average power factor lower than 0.9.
The contracts applied are different from country to country and can vary also according to the typology of costumer: as a consequence, the following remarks are to be considered as a mere didactic and indicative information aimed at showing the economic saving which can be obtained thanks to the power factor correction.
Generally speaking, the power supply contractual clauses require the payment of the absorbed reactive energy when the power factor is included in the range from 0.7 and 0.9, whereas nothing is due if it is higher than 0.9. For cosϕ < 0.7 power supply authorities can oblige consumers to carry out power factor correction.
It is to be noted that having a monthly average power factor higher than or equal to 0.9 means requesting from the network a reactive energy lower than or equal to 50% of the active energy:
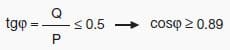
Therefore no penalties are applied if the requirements for reactive energy do not exceed 50% of the active one.
The cost that the consumer bears on a yearly base when drawing a reactive energy exceeding that corresponding to a power factor equal to 0.9 can be expressed by the following relation:
![]()
where:
- CEQ is the cost of the reactive energy per year in €;
- EQ is the reactive energy consumed per year in kvarh;
- EP is the active energy consumed per year in kWh;
- EQ – 0.5 · Ep is the amount of reactive energy to be paid;
- c is the unit cost of the reactive energy in €/kvarh.
If the power factor is corrected at 0.9 not to pay the consumption of reactive energy, the cost of the capacitor bank and of the relevant installation will be:
![]()
where:
- CQc is the yearly cost in € to get a power factor equal to 0.9;
- Qc is the power of the capacitor bank necessary to have a cosϕ of 0.9, in kvar;
- cc is the yearly installation cost of the capacitor bank in €/kvar.
The saving for the consumer shall be:
![]()
It is necessary to note that the capacitor bank represents an “installation cost” to be divided suitably for the years of life of the installation itself applying one or more economic coefficients; in the practice, the savings obtained by correcting the power factor allow the payback of the installation cost of the capacitor bank within the first years of use.
As a matter of fact, an accurate analysis of an investment implies the use of some economic parameters that go beyond the purposes of this Technical Application Paper.
Example
A company absorbs active and reactive energy according to table 1:

1 0.484 is the tangent corresponding to a cosϕ equal to 0.9
If an automatically-controlled capacitor bank for power factor correction with Qc=30 kvar, against a total installation cost per year cc of 25 €/kvar, a total cost of 750 € is obtained. The saving for the consumer, without keeping into account the payback and the financial charges, shall be:

1 0.484 is the tangent corresponding to a cosϕ equal to 0.9
If an automatically-controlled capacitor bank for power factor correction with Qc=30 kvar, against a total installation cost per year cc of 25 €/kvar, a total cost of 750 € is obtained. The saving for the consumer, without keeping into account the payback and the financial charges, shall be:
![]()











Great post on power factor correction, very technical but i followed it great, thanks for posting